题目内容
【题目】正方形ABCD中，在AB边上有一定点E，AE=3cm，EB=1cm，在AC上有一动点P，若使得EP+BP的和最小，则EP+BP的最短距离为 ．
A.5cm
B.4 cm
C.3cm
D.4．8cm
【答案】A
【解析】如图所示：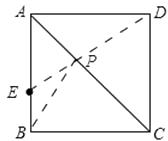 
∵四边形ABCD是正方形，
∴点B与点D关于AC对称，连接ED交AC与点P，
∴PB=PD．
∴PE+PB=PD+EP．由两点之间线段最短可知：当点E、P、D在一条直线上时，PE+PB有最小值，最小值为ED，
∵AE=3cm，EB=1cm，
∴AD=4，
∴在Rt△ADE中，ED= 
，
所以答案是：A．
【考点精析】利用轴对称的性质对题目进行判断即可得到答案，需要熟知关于某条直线对称的两个图形是全等形；如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上．
练习册系列答案
相关题目
