题目内容
.(13分)已知抛物线y=ax 2+bx+c经过O(0,0),A(4,0),B(3,)三点,连接AB,过点B作BC∥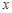 轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
(1)求抛物线的解析式;
(2)记△EFA的面积为S,求S关于t的函数关系式,并求S的最大值,指出此时△EFA的形状;
 (3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
(3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
【答案】
见解析
【解析】
(1)根据题意得
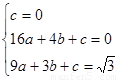 解得:
解得: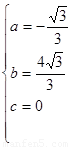

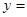

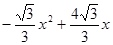 ------------4分
------------4分
(2)过点B作BM⊥x轴于M,
则BM=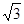 ,OM=3,∵OM=4,∴AM=1
,OM=3,∵OM=4,∴AM=1
AB=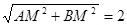
∵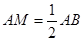 ∴∠BAM=60°
∴∠BAM=60°
当0<t《2时,AF=t,过点F作FH⊥x轴,
 ∵FN=Afsin60°=
∵FN=Afsin60°=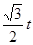 ,
,
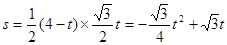
当2<t《4时,如图,
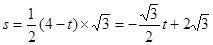
 当0<t《2时,当
当0<t《2时,当
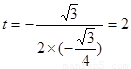 时,
时,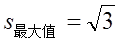
当2<t《4时,s<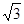
∴当x=2时,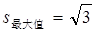
,此时AE=AF=2又∵∠EAF=60°. ∴△AEF为等边三角形. -----------10分
(3)当0≤t≤2时,
若∠EFA=90°,此时∠FEA=30°, ∴EA=2AF,4-t=2t, ∴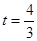 .此时E
.此时E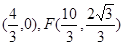
当∠FEA=90°时,此时∠EFA=30°, ∴2EA=AF,∴t=2(4-t)
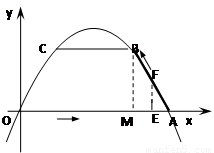 ∴
∴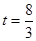 >2,
∴这种情况不存在。
>2,
∴这种情况不存在。
当2<t《4时,有t-2+t=3
∴t=2.5
E(2.5,0), F(2.5,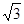 ).
------------13分
).
------------13分

练习册系列答案
相关题目
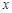 轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒).
轴交抛物线于点C.动点E、F分别从O、A两点同时出发,其中点E沿线段OA以每秒1个单位长度的速度向A点运动,点F沿折线A→B→C以每秒1个单位长度的速度向C点运动.设动点运动的时间为t(秒). (3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由.
(3)是否存在这样的t值,使△EFA是直角三角形?若存在,求出此时E、F两点的坐标;若不存在,请说明理由. +bx+c与
+bx+c与 轴交于
轴交于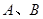 两点,若
两点,若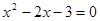 的两个实数根,与
的两个实数根,与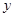 轴交于点
轴交于点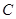 (0,3),
(0,3),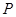 ,使
,使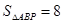 .
.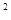 +bx+c与
+bx+c与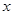 轴交于
轴交于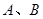 两点,若
两点,若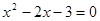 的两个实数根,与
的两个实数根,与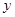 轴交于点
轴交于点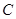 (0,3),
(0,3), ,使
,使 .
.