Question

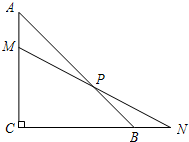（2006•上海模拟）如图，已知等腰直角三角形ABC中，∠C=90°，AC=2，M是边AC上一点，过点M的直线交CB的延长线于点N，交边AB于点P，且AM=BN．
（1）求证：MP=NP；
（2）设AM=x，四边形MCBP的面积为y，求y与x的函数解析式，并写出函数的定义域；
（3）探索：以线段CM为直径的圆能否与边AB相切？如果能够相切，请求出x的值；如果不能相切，请说明理由．

Answer 1

分析：（1）作辅助线MQ（过点M作MQ∥CN，交AB于点Q），构建全等三角形：△MQP≌△NBP；然后根据全等三角形的对应边相等即可证得MP=NP；
（2）过点P作PD⊥CN，垂足为点D．利用等腰直角三角形的性质求得AM=BN=x，MC=2-x，PD=

1

2

（2-x）；利用“割补法”知，y=S_△MNC-S_△BNP=-

1

4

x²-

1

2

x+2，该函数的定义域即根据AC边的长度来设定；
（3）设以线段CM为直径的圆的圆心为O，过点O作OF⊥AB，垂足为点F．要使以线段CM为直径的圆能与边AB相切，必须有OF=

1

2

CM，据此列出关于x的方程，通过解该方程即可求得x的值．

解答：解：（1）证明：过点M作MQ∥CN，交AB于点Q． 
∵AC=BC，∠C=90°，∴∠A=45°．
∵MQ∥CN，∴∠AMQ=∠C=90°．
∴∠AQM=∠A=45°．
∴AM=MQ． 
∵AM=BN，∴MQ=BN．
∵MQ∥CN，∴∠QMP=∠N，∠MQP=∠NBP，
∵MQ=BN，
∴△MQP≌△NBP． 
∴MP=NP；

（2）过点P作PD⊥CN，垂足为点D．
∴PD∥AC．
∵由（1）知，MP=NP，
∴PD=

1

2

MC． 
∵AM=BN=x，
∴MC=2-x，PD=

1

2

（2-x）． 
∴y=S_△MNC-S_△BNP=

1

2

（2-x）（2+x）-

1

2

x•

1

2

（2-x）=-

1

4

x²-

1

2

x+2，
即所求的函数解析式为y=-

1

4

x²-

1

2

x+2，
定义域为0＜x＜2．

（3）设以线段CM为直径的圆的圆心为O，过点O作OF⊥AB，垂足为点F． 
∵AO=x+

1

2

（2-x）=

1

2

x+1，∠A=45°，
∴OF=

2

2

（

1

2

x+1）．
∵要使以线段CM为直径的圆能与边AB相切，必须有OF=

1

2

CM=

1

2

（2-x），
∴

2

2

(

1

2

x+1)=

1

2

(2-x)． 

2

2

（

1

2

x+1）=

1

2

（2-x），
解得，x=6-4

2

，
即当x=6-4

2

时，线段CM为直径的圆能与边AB相切．

点评：本题考查了圆的综合题．此题涉及到的知识点有：勾股定理、等腰直角三角形的判定与性质、全等三角形的判定与性质以及切线的性质．