题目内容
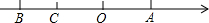如图，数轴上A，B，C表示实数a，b，c，化简|a+b|-
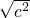，正确的是
- A.a+b-c
- B.a-b+c
- C.-a-b+c
- D.-a-b-c
C
分析：根据数轴上点的位置判断出a+b与c的正负，利用绝对值及二次根式的化简公式计算即可得到结果．
解答：由数轴上点的位置得：b＜c＜0＜a，|a|＜|b|，
∴a+b＜0，
则|a+b|-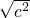=-a-b-|c|=-a-b+c．
故选C
点评：此题考查了二次根式的性质与化简，以及实数与数轴，判断出a+b及c的正负是解本题的关键．
分析：根据数轴上点的位置判断出a+b与c的正负，利用绝对值及二次根式的化简公式计算即可得到结果．
解答：由数轴上点的位置得：b＜c＜0＜a，|a|＜|b|，
∴a+b＜0，
则|a+b|-
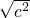=-a-b-|c|=-a-b+c．故选C
点评：此题考查了二次根式的性质与化简，以及实数与数轴，判断出a+b及c的正负是解本题的关键．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图，数轴上两个点表示的数分别为a，b，则
如图，数轴上A，B，C表示实数a，b，c，化简|a+b|-
如图，数轴上的三点A、B、C分别表示有理数a、b、c，则化简|a-b|-|c-a|+|b-c|=
如图，数轴上点A表示-5、点B表示3．①AB的长度为
如图，数轴上与点M的距离为2的点表示的数是