Question

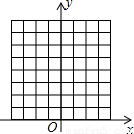
在8×8的正方形网格中建立如图所示的平面直角坐标系，已知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形．
（1）填空：C点的坐标是______，△ABC的面积是______；
（2）将△ABC绕点C旋转180°得到△A₁B₁C₁，连接AB₁、BA₁，试判断四边形AB₁A₁B是何种特殊四边形，请说明理由；
（3）请探究：在x轴上是否存在这样的点P，使四边形ABOP的面积等于△ABC面积的2倍？若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．

Answer 1

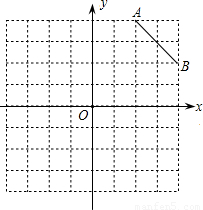
【答案】分析：（1）此点应在AB的垂直平分线上，在第一象限，腰长又是无理数，只有是点（1，1），从A，B向x轴引垂线，把所求的三角形的面积分为一个直角三角形和一个直角梯形的面积减去一个直角三角形的面积．
（2）旋转180°后可得新四边形的对角线互相平分，那么先判断是平行四边形，然后根据等腰三角形的性质得到对角线相等，那么所求的四边形是矩形．
（3）根据平行四边形的性质，结合（1）中的方法解答．
解答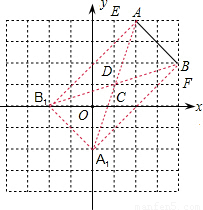：解：（1）（1，1），4；

（2）四边形AB₁A₁B是矩形．
∵AC=A₁C，BC=B₁C，AC=BC
∴AA₁=BB₁
∴四边形AB₁A₁B是矩形

（3）∵S_△ABC=S_梯形ABDE+S_矩形BDCF-（S_△AEC+S_△BCF）=×（1+3）×2+3×1-×1×3-×1×3=4，
∴四边形ABOP的面积等于8．
同（1）中的方法得到三点A，B，O构成的面积为6．当P在O左边时，△APO的面积应为2，高为4，那么底边长为1，所以P（-1，0）；
当P在O右边时，△BOP的面积应为2，高为2，所以底边长为2，此时P坐标为（2，0）．
故点P的坐标为（2，0），（-1，0）．
点评：到一条线段两个端点距离相等的点在这条线段的垂直平分线上．对角线互相平分且相等的四边形是平行四边形．