题目内容
(2010•扬州二模)(1)如图1,已知∠AOB,OA=OB,点E在OB边上,四边形AEBF是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线;(保留作图痕迹,不要求写作法)(2)如图2,在10×10的正方形网格中,点A(0,0)、B(5,0)、C(3,6)、D(-1,3),
①依次连接A、B、C、D四点得到四边形ABCD,四边形ABCD的形状是______;
②在x轴上找一点P,使得△PCD的周长最短(直接画出图形,不要求写作法),此时,点P的坐标为______,最短周长为______
【答案】分析:(1)根据平行四边形的性质可知∠AOB的平分线必定经过平行四边形的中心即对角线的交点.所以先做平行四边形的对角线,再作∠AOB的平分线.
(2)在x轴上找一点P,使得△PCD的周长最短,即PD+PC最小,所以可先做点D关于x轴的对称点D′,连接CD′,与x轴相交于点P.所以P( ,0),最短周长为
,0),最短周长为 .
.
解答: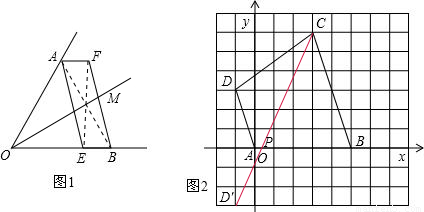
解:(1)如图所示;(2分)
(2)①等腰梯形;(4分)
②D关于x轴的对称点D′,连接CD′,则D′(-1,-3),
设过点CD′的直线解析式为:y=kx+b(k≠0),把C、D′两点坐标代入得,
 ,解得
,解得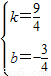 ,
,
故直线CD′的解析式为:y= x-
x- ,
,
当y=0时,x= ,
,
故P点坐标为:( ,0)
,0)
故答案为:P( ,0);
,0);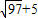 (其中画图正确得2分)(10分)
(其中画图正确得2分)(10分)
点评:主要考查了复杂作图和轴对称作图.熟悉平行四边形的性质和轴对称的性质是解题的关键.
(2)在x轴上找一点P,使得△PCD的周长最短,即PD+PC最小,所以可先做点D关于x轴的对称点D′,连接CD′,与x轴相交于点P.所以P(
 ,0),最短周长为
,0),最短周长为 .
.解答:

解:(1)如图所示;(2分)
(2)①等腰梯形;(4分)
②D关于x轴的对称点D′,连接CD′,则D′(-1,-3),
设过点CD′的直线解析式为:y=kx+b(k≠0),把C、D′两点坐标代入得,
 ,解得
,解得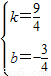 ,
,故直线CD′的解析式为:y=
 x-
x- ,
,当y=0时,x=
 ,
,故P点坐标为:(
 ,0)
,0)故答案为:P(
 ,0);
,0); (其中画图正确得2分)(10分)
(其中画图正确得2分)(10分)点评:主要考查了复杂作图和轴对称作图.熟悉平行四边形的性质和轴对称的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2010•扬州二模)如图,早上10点小东测得某树的影长为2m,到了下午5时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度约为
(2010•扬州二模)如图,早上10点小东测得某树的影长为2m,到了下午5时又测得该树的影长为8m,若两次日照的光线互相垂直,则树的高度约为
