题目内容
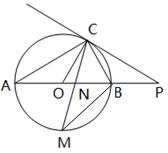
(本题满分12分) 如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
【小题1】(1)求证:PC是⊙O的切线;
【小题2】(2)求∠P的度数;
【小题3】(3)点M是弧AB的中点,CM交AB于点N,AB=4,求线段BM、CM及弧BC所围成的图形面积。
【小题1】(1)∵OA=OC,∴∠A=∠ACO
∵∠COB=2∠A ,∠COB=2∠PCB
∴∠A=∠ACO=∠PCB ……………………………………………………1分
∵AB是⊙O的直径
∴∠ACO+∠OCB=90° …………………………………………………2分
∴∠PCB+∠OCB=90°,即OC⊥CP …………………………………………3分
 ∵OC是⊙O的半径
∵OC是⊙O的半径 ∴PC是⊙O的切线
【小题2】(2)∵PC="AC " ∴∠A=∠P
|
|
 ∵∠A+∠ACO+∠PCO+∠P=180°
∵∠A+∠ACO+∠PCO+∠P=180°∴3∠P=90°
∴∠P=30°
【小题3】(3) ∵点M是半圆O的中点 ∴∠BCM=45°………7分
由(2)知∠BMC=∠A=∠P=30°∴BC=
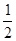 AB="2" ……8分
AB="2" ……8分作BD⊥CM于D,∴CD=BD=
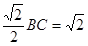 ∴DM=
∴DM=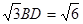
∴CM=
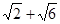 …………………9分
…………………9分∴S△BCM=
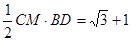 ………………10分
………………10分∵∠BOC=2∠A=60° ∴弓形BmC的面积=
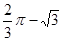 …………11分
…………11分∴线段BM、CM及弧BC所围成的图形面积为
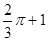 解析:
解析:略

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目


 分别交
分别交 轴,
轴, 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形. 个单位长度的速度向终点B运动,过点P作
个单位长度的速度向终点B运动,过点P作 ,垂足为H,连接
,垂足为H,连接 ,
, .设点P的运动时间为
.设点P的运动时间为 秒.
秒. 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.

 =4
=4 ,求△ABC的周长.
,求△ABC的周长. 、
、 (千米)与行驶时间
x(时)的关系如图②所示.
(千米)与行驶时间
x(时)的关系如图②所示. 
 ,乙的速度为
,乙的速度为