题目内容
【题目】如图所示,已知AB∥CD,分别探究下面图形中∠APC,∠PAB,∠PCD的关系,请你从四个图形中任选一个,说明你所探究的结论的正确性.
①结论:(1)
(2)
(3)
(4)
②选择结论 (1) , 说明理由.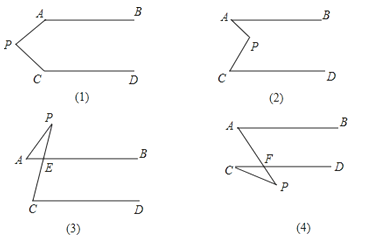
【答案】∠APC+∠PAB+∠PCD=360°;∠APC=∠PAB+∠PCD;∠PCD=∠APC+∠PAB;∠PAB=∠APC+∠PCD
【解析】解: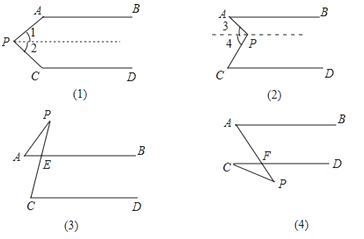
①(1)过点P作PE∥AB,则AB∥PE∥CD,
∴∠1+∠PAB=180°,
∠2+∠PCD=180°,
∴∠APC+∠PAB+∠PCD=360°;
(2)过点P作直线l∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠PAB=∠3,∠PCD=∠4,
∴∠APC=∠PAB+∠PCD;
(3)∵AB∥CD,
∴∠PEB=∠PCD,
∵∠PEB是△APE的外角,
∴∠PEB=∠PAB+∠APC,
∴∠PCD=∠APC+∠PAB;
(4)∵AB∥CD,
∴∠PAB=∠PFD,
∵∠PFD是△CPF的外角,
∴∠PCD+∠APC=∠PFD,
∴∠PAB=∠APC+∠PCD.
②选择结论(1),证明同上.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
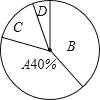
课程达标测试卷闯关100分系列答案【题目】某校举行九年级体育锻炼考试,现随机抽取了部分学生的成绩为样本,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面两图不完整的统计图和统计表:
等级 | 成绩(分) | 频数(人数) | 频率 |
A | 45~50 | 40 | 0.4 |
B | 40~44 | 42 | x |
C | 35~39 | m | 0.12 |
D | 30~34 | 6 | 0.03 |
合计 | 1.00 |
请根据以如图表提供的信息,解答下列问题:
(1)m= ,x= ;
(2)在扇形统计图中,B等级所对应的圆心角是 度;
(3)若该校九年级共有600名学生参加了体育模板考试,请你估计成绩等级达到“优秀”的学生有 人;
(4)小明同学第一次模拟考试成绩为40分,第二次成绩为48分,则小明体育成绩提高的百分率是 %.