题目内容
 20、如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.求∠PAQ的度数.
20、如图所示,∠BAC=105°,若MP和NQ分别垂直平分AB和AC.求∠PAQ的度数.分析:先根据三角形内角和等于180°求出∠ABP+∠ACQ=75°,再根据线段垂直平分线的性质∠PAB=∠ABP,∠QAC=∠ACQ,所以∠PAB+∠QAC=75°,便不难求出∠PAQ的度数为30°.
解答:解:∵∠BAC=105°,
∴∠ABP+∠ACQ=180°-105°=75°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=75°,
∴∠PAQ=105°-75°=30°.
∴∠ABP+∠ACQ=180°-105°=75°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=75°,
∴∠PAQ=105°-75°=30°.
点评:本题主要利用三角形内角和定理和线段垂直平分线的性质求解.

练习册系列答案
相关题目
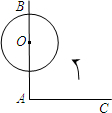 如图所示,∠BAC=90°,O为AB上一点,以O为圆心,
如图所示,∠BAC=90°,O为AB上一点,以O为圆心,| 1 |
| 2 |
| A、30° | B、60° |
| C、60°或120° | D、120° |
 5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )
5、如图所示,∠BAC=90°,AB=AC,过点A任意作一直线DE,且作CE⊥ED,BD⊥ED,经测量CE=2cm,BD=4cm,则DE的长为( )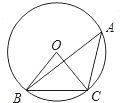 如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB=
如图所示,∠BAC是⊙O的圆周角,则∠BAC+∠OCB= 19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
19、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.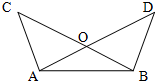 18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,
18、如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,