题目内容
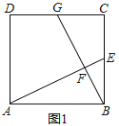
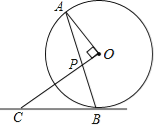
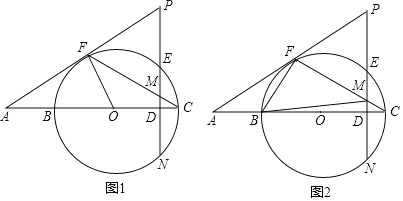
【题目】如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=![]() ∠P.
∠P.
(1)求证:PA是⊙O的切线;
(2)若∠A=30°,⊙O的半径为4,DM=1,求PM的长;
(3)如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C为顶点的三角形与△BFM相似,求DH的长度.
【答案】(1)证明见解析;(2)PM=4![]() ﹣2;(3)满足条件的DH的值为
﹣2;(3)满足条件的DH的值为![]() 或
或![]() .
.
【解析】
(1)如图1中,作PH⊥FM于H.想办法证明∠PFH=∠PMH,∠C=∠OFC,再根据等角的余角相等即可解决问题;
(2)解直角三角形求出AD,PD即可解决问题;
(3)分两种情形①当△CDH∽△BFM时,![]() .
.
②当△CDH∽△MFB时,![]() ,分别构建方程即可解决问题;
,分别构建方程即可解决问题;
(1)证明:如图1中,作PH⊥FM于H.

∵PD⊥AC,∴∠PHM=∠CDM=90°,∵∠PMH=∠DMC,∴∠C=∠MPH,
∵∠C=![]() ∠FPM,∴∠HPF=∠HPM,
∠FPM,∴∠HPF=∠HPM,
∵∠HFP+∠HPF=90°,∠HMP+∠HPM=90°,∴∠PFH=∠PMH,
∵OF=OC,∴∠C=∠OFC,
∵∠C+∠CMD=∠C+∠PMF=∠C+∠PFH=90°,
∴∠OFC+∠PFC=90°,∴∠OFP=90°,
∴直线PA是⊙O的切线.
(2)解:如图1中,∵∠A=30°,∠AFO=90°,∴∠AOF=60°,
∵∠AOF=∠OFC+∠OCF,∠OFC=∠OCF,∴∠C=30°,
∵⊙O的半径为4,DM=1,
∴OA=2OF=8,CD=![]() DM=
DM=![]() ,
,
∴OD=OC﹣CD=4﹣![]() ,
,
∴AD=OA+OD=8+4﹣![]() =12﹣
=12﹣![]() ,
,
在Rt△ADP中,
DP=ADtan30°=(12﹣![]() )×
)×![]() =4
=4![]() ﹣1,
﹣1,
∴PM=PD﹣DM=4 ![]() ﹣2.
﹣2.
(3)如图2中,
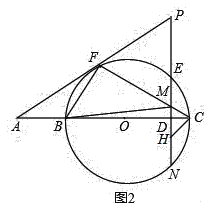
由(2)可知:BF=![]() BC=4,FM=
BC=4,FM=![]() BF=4
BF=4![]() ,CM=2DM=2,CD=
,CM=2DM=2,CD=![]() ,
,
∴FM=FC﹣CM=4![]() ﹣2,
﹣2,
①当△CDH∽△BFM时,![]() ,
,
∴ ![]() ,∴DH=
,∴DH=![]()
②当△CDH∽△MFB时,![]() ,
,
∴![]() ,∴DH=
,∴DH=![]() ,
,
∵DN=![]() ,
,
∴DH<DN,符合题意,
综上所述,满足条件的DH的值为![]() 或
或![]() .
.