题目内容
【题目】如图,正方形ABCD的边长为4,点E是AB的中点,点P是边BC上的动点,点Q是对角线AC上的动点(包括端点A,C),则EP+PQ的最小值是 . 
【答案】![]()
【解析】如图作点E关于BC的对称点E′,作E′Q′⊥AC于Q′交BC于P.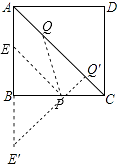
∴PE=PE′,
∴PQ+PE=PE′+PQ,
当Q用Q′重合时,PE+PQ最小(垂线段最短),
∵四边形ABCD是正方形,
∴∠E′AQ′=45°,
∵AE′=6,
∴E′Q′=3 ![]()
∴PE+PQ的最小值为3 ![]() .
.
【考点精析】利用勾股定理的概念和正方形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
相关题目
