题目内容
在一次测量旗杆高度的活动中,某小组使用的方案如下:
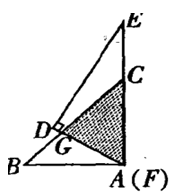
如图,AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面,若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度.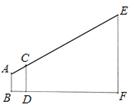
如图,AB表示某同学从眼睛到脚底的距离,CD表示一根标杆,EF表示旗杆,AB、CD、EF都垂直于地面,若AB=1.6m,CD=2m,人与标杆之间的距离BD=1m,标杆与旗杆之间的距离DF=30m,求旗杆EF的高度.

14米
试题分析:过点A作AH⊥EF于H点,AH交CD于G,根据CD∥EF可得△ACG∽△AEH,根据相似三角形的性质可求得EH的长,从而求得结果.
过点A作AH⊥EF于H点,AH交CD于G
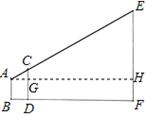
∵CD∥EF
∴△ACG∽△AEH
∴
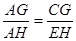 ,即
,即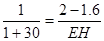
∴EH=12.4
∴EF=EH+HF=12.4+1.6=14
∴旗杆的高度为14米.
点评:解直角三角形的应用是中考必考题,一般难度不大,正确作出辅助线构造直角三角形是解题关键.

练习册系列答案
相关题目
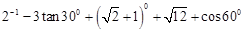
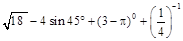 .
.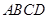 中,
中,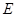 、
、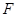 分别为
分别为 、
、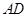 的中点,若
的中点,若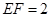 ,
,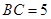 ,
, ,则
,则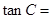 .
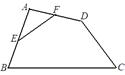
.
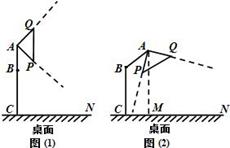
 )
)
 cm2
cm2
 )cm2
)cm2
