题目内容
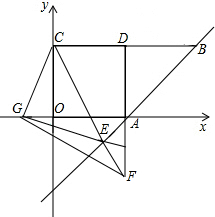
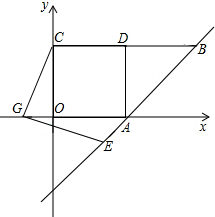
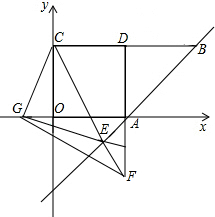
已知,如图在正方形OADC中,点C的坐标为(0,4),点A的坐标为(4,0),CD的延长线交双曲线y=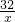 于点B.
于点B.
(1)求直线AB的解析式;

(2)G为x轴的负半轴上一点连接CG,过G作GE⊥CG交直线AB于E.求证CG=GE;
(3)在(2)的条件下,延长DA交CE的延长线于F,当G在x的负半轴上运动的过程中,请问 的值是否为定值,若是,请求出其值;若不是,请说明你的理由.
的值是否为定值,若是,请求出其值;若不是,请说明你的理由.
解:(1)设y=kx+b,
∵点C的坐标为(0,4),BC∥X轴,
∴点B纵坐标为4,
当y=4时,x=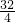 =8,
=8,
根据题意得 ,
,
∴k=1,b=-4,
∴y=x-4;

(2)在y轴的负半轴上取一点F,使得OF=OG,连接GF,
∵CO=AO,
∴CF=AG,
∵GE⊥CG,∠GOC=90°,
∴∠GCO=∠AGE
而∠GAE=∠GFO=45°,
∴△CGF≌△AGE,
∴CG=GE;
(3)答:是定值为1.
证明:在DF上取一点N,使得DN=OG,连接CN,
∵CO=CD,DN=GO,∠COG=∠CDN=90°,
∴△CGO≌△CND,
∴CN=CG,∠GCO=∠DCN,
又∠OCN+∠DCN=90°,
∴∠GCN=∠GCO+∠OCN=∠DCN+∠OCN=90°,
∵GC=GE,∠CGE=90°,
∴∠GCF=45°,又∠GCN=90°,
∴∠GCF=∠NCF=45°,而CF公共,
∴△CGF≌△CNF,则GF=NF,
则 =
=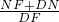 =
=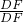 =1.
=1.
分析:(1)欲求直线AB的解析式,须知点A B坐标,已知A坐标,只求B坐标.由于BC∥X轴可以得到点B纵坐标为4,代入y=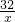 中可求出点B横坐标;
中可求出点B横坐标;
(2)欲证CG=GE,利用原图无法证出,须作辅助线构建三角形全等,因此在y轴的负半轴上取一点F,使得OF=OG,连接GF可证△CGF≌△AGE,即解.
点评:此题综合性比较强,主要考查一次函数的图形和性质、反比例函数的图象和性质,正方形的性质及全等三角形的性质和判定.
∵点C的坐标为(0,4),BC∥X轴,
∴点B纵坐标为4,
当y=4时,x=
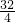 =8,
=8,根据题意得
 ,
,∴k=1,b=-4,
∴y=x-4;

(2)在y轴的负半轴上取一点F,使得OF=OG,连接GF,
∵CO=AO,
∴CF=AG,
∵GE⊥CG,∠GOC=90°,
∴∠GCO=∠AGE
而∠GAE=∠GFO=45°,
∴△CGF≌△AGE,
∴CG=GE;
(3)答:是定值为1.
证明:在DF上取一点N,使得DN=OG,连接CN,
∵CO=CD,DN=GO,∠COG=∠CDN=90°,

∴△CGO≌△CND,
∴CN=CG,∠GCO=∠DCN,
又∠OCN+∠DCN=90°,
∴∠GCN=∠GCO+∠OCN=∠DCN+∠OCN=90°,
∵GC=GE,∠CGE=90°,
∴∠GCF=45°,又∠GCN=90°,
∴∠GCF=∠NCF=45°,而CF公共,
∴△CGF≌△CNF,则GF=NF,
则
 =
=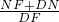 =
=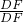 =1.
=1.分析:(1)欲求直线AB的解析式,须知点A B坐标,已知A坐标,只求B坐标.由于BC∥X轴可以得到点B纵坐标为4,代入y=
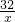 中可求出点B横坐标;
中可求出点B横坐标;(2)欲证CG=GE,利用原图无法证出,须作辅助线构建三角形全等,因此在y轴的负半轴上取一点F,使得OF=OG,连接GF可证△CGF≌△AGE,即解.
点评:此题综合性比较强,主要考查一次函数的图形和性质、反比例函数的图象和性质,正方形的性质及全等三角形的性质和判定.

练习册系列答案
相关题目
 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处. 已知:如图,正方形ABCD的边长为9,M在BC上,MC=6,在AC上找一个点P,使BP+MP最小值,求出最小值为多少?(要求画出图形,进行计算,不要求证明)
已知:如图,正方形ABCD的边长为9,M在BC上,MC=6,在AC上找一个点P,使BP+MP最小值,求出最小值为多少?(要求画出图形,进行计算,不要求证明)