题目内容
【题目】如图，A（0，4）是直角坐标系y轴上一点，动点P从原点O出发，沿x轴正半轴运动，速度为每秒1个单位长度，以P为直角顶点在第一象限内作等腰Rt△APB．设P点的运动时间为t秒．
（1）若AB//x轴，如图一，求t的值；
（2）当t=3时，坐标平面内有一点M（不与A重合） ， 使得以M、P、B为顶点的三角形和△ABP全等，请直接写出点M的坐标；
（3）设点A关于x轴的对称点为 
,连接 
，在点P运动的过程中，∠ 
的度数是否会发生变化，若不变，请求出∠ 的度数，若改变，请说明理由。
【答案】
（1）解：过点B作BC⊥x轴于点C，如图1所示．
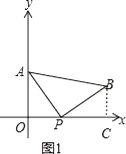
∵AO⊥x轴，BC⊥x轴，且AB//x轴，
∴四边形ABCO为长方形，
∴AO=BC=4．
∵△APB为等腰直角三角形，
∴AP=BP，∠PAB=∠PBA=45°，
∴∠OAP=90°﹣∠PAB=45°，
∴△AOP为等腰直角三角形，
∴OA=OP=4．
t=4÷1=4（秒），
故t的值为4
（2）解：点M的坐标为（4，7）, （6，-4）, （10，-1）
（3）解： 
∵△APB为等腰直角三角形，
∴∠APO+∠BPC=180°﹣90°=90°．
又∵∠PAO+∠APO=90°，
∴∠PAO=∠BPC．
在△PAO和△BPC中，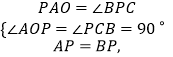 
∴△PAO≌△BPC，
∴AO=PC，BC=PO．
∵点A（0，4），点P（t，0）
∴PC=AO=4，BC=PO=t，CO=PC+PO=4+ t
∴点 
∴过点 
作 
轴于点 
，
为等腰直角三角形.
∴∠ 
=45°
【解析】 （1）过点B作BC⊥x轴于点C，如图1所示．根据题意首先判断出四边形ABCO为长方形，然后根据矩形的性质得出AO=BC，根据等腰直角三角形的性质知AP=BP，∠PAB=∠PBA=45°，从而得出∠OAP=45°，进而判断出△AOP为等腰直角三角形，根据等腰直角三角形的性质得出OA=OP=4，然后根据时间=路程除以速度算出结果；
（2）当t=3时OP=3，又OA=4，根据勾股定理得出AP的长，根据等腰直角三角形的意义得出AP=BP，再根据勾股定理得出AB的长，然后分类讨论当△MPB和△ABP全等时，易得点M的坐标为（4，7）, （10，-1）；当△MPB与△APB全等时，此时点M与点A关于点P 对称易得点M的坐标为（6，-4）, 综上所述从而得出答案；
（3） 根据等腰直角三角形的性质及同角的余角相等得出∠PAO=∠BPC，然后利用SAS判断出△PAO≌△BPC，根据全等三角形对应边相等得出AO=PC，BC=PO，根据A,P两点的坐标表示出PC=AO=4，BC=PO=t，CO=PC+PO=4+ t，从而得出b点的坐标，过点 B 作 B H ⊥ y 轴于点 H ，BH=OC=4+t=A′H,判断出△ A ′ H B 为等腰直角三角形，得出结论。
【考点精析】认真审题，首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°)．
