题目内容
14、已知，如图，在平行四边形ABCD中，E、F分别是AD、BC的中点．求证：
（1）△ABE≌△CDF；
（2）BE=DF．
分析：（1）要证明△ABE≌△CDF，根据平行四边形的性质，易证AB=CD，∠A=∠C，AE=CF，利用SAS可证得两三角形全等．
（2）由（1）的结论可以直接得到．
（2）由（1）的结论可以直接得到．
解答：解：（1）∵四边形ABCD是平行四边形，
∴∠A=∠C，AB=CD，AD=BC．
又∵E、F分别是AD、BC的中点，
∴AE=CF．
∴△ABE≌△CDF．
（2）由△ABE≌△CDF，得BE=DF．
∴∠A=∠C，AB=CD，AD=BC．
又∵E、F分别是AD、BC的中点，
∴AE=CF．
∴△ABE≌△CDF．
（2）由△ABE≌△CDF，得BE=DF．
点评：三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
练习册系列答案
相关题目
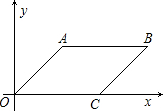如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，