题目内容
 如图,若AE是△ABC边上的高,∠EAC的角平分线AD交BC于D,∠ACB=40°,求∠DAE.
如图,若AE是△ABC边上的高,∠EAC的角平分线AD交BC于D,∠ACB=40°,求∠DAE.考点:三角形内角和定理
专题:计算题
分析:根据直角三角形两锐角互余求出∠CAE,再根据角平分线的定义可得∠DAE=
∠CAE.
| 1 |
| 2 |
解答:解:∵AE是△ABC边上的高,∠ACB=40°,
∴∠CAE=90°-∠ACB=90°-40°=50°,
∴∠DAE=
∠CAE=
×50°=25°.
∴∠CAE=90°-∠ACB=90°-40°=50°,
∴∠DAE=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,角平分线的定义,是基础题,熟记定理与概念并准确识图是解题的关键.

练习册系列答案
相关题目
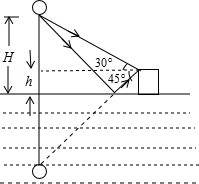 如图,在湖边一座楼房顶上观察湖面上空一只悬浮的气球,直接观察时,仰角 α=30°,观察湖中气球倒影时,俯角为β=45°,房顶离湖面高度为h=10m,求气球离湖面的高度H.
如图,在湖边一座楼房顶上观察湖面上空一只悬浮的气球,直接观察时,仰角 α=30°,观察湖中气球倒影时,俯角为β=45°,房顶离湖面高度为h=10m,求气球离湖面的高度H. 观察有理数a、b、c在数轴上的位置并化简:|b-c|+|a+c|.
观察有理数a、b、c在数轴上的位置并化简:|b-c|+|a+c|.