��Ŀ����
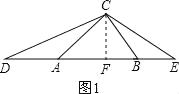
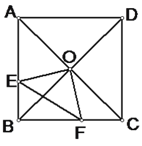
����Ŀ����1����ͼ��1��������ABC�У�AB��AC��BC����ACB=80������D��E�ֱ����߶�BA��AB���ӳ����ϣ���AD=AC��BE=BC������DCE= ��
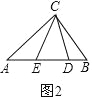
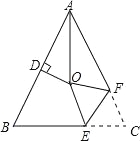
��2����ͼ��2��������ABC�У�AB��AC��BC����ACB=80������D��E�ֱ��ڱ�AB�ϣ���AD=AC��BE=BC������DCE�Ķ�����
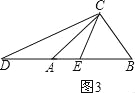
��3������ABC�У�AB��AC��BC����ACB=80������D��E�ֱ���ֱ��AB�ϣ���AD=AC��BE=BC��������DCE�Ķ�����ֱ��д���𰸣���
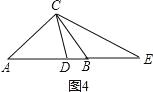
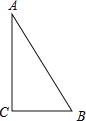
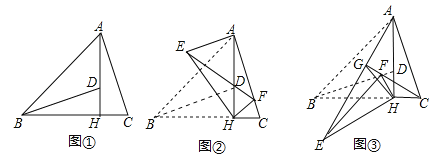
��4����ͼ��3��������ABC�У�AB=14��AC=15��BC=13����D��E��ֱ��AB�ϣ���AD=AC��BE=BC������������ͼ�β�������������ͼ�ε��·�ֱ��д����DCE�������������ж��������ͼ�β��������Լ����������������һ��ͼ�ε�����ʾ����
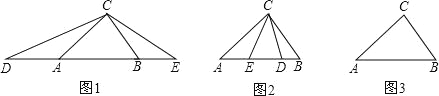
���𰸡�(1)��130����(2)��50����(3)��40����(4)��252��84��96��72.
��������
���������(1)�����ݵ��������ε����ʵõ���ACD=��D����BCE=��E���������ε��ڽǺ͵õ���CAB+��CBA=100�������������ε���ǵ����ʵõ���CDA+��BCE=![]() ����CAB+��CBA��=50�������ɵõ����ۣ�
����CAB+��CBA��=50�������ɵõ����ۣ�
(2)�����������ε��ڽǺͺ���ǵ����ʼ��ɵõ����ۣ�(3)����D��E�ֱ���ֱ��AB�ϣ���ȥ��1����2��������������������������ͼ3����(1)֪����D=![]() CAB���ɣ�2��֪��CEB=
CAB���ɣ�2��֪��CEB=![]() ���з��̼�����ý������4������ABC�У�AB=14��AC=15��BC=13����C��CF��AB��F�����ݹ��ɶ������AB���ϵĸ�CF=12��Ȼ����������ε������ʽ����ǿ��Ľ��ۣ�
���з��̼�����ý������4������ABC�У�AB=14��AC=15��BC=13����C��CF��AB��F�����ݹ��ɶ������AB���ϵĸ�CF=12��Ȼ����������ε������ʽ����ǿ��Ľ��ۣ�
���������(1)����AD=AC��BE=BC�� ���ACD=��D����BCE=��E�� �ߡ�ACB=80����
���CAB+��CBA=100���� ���CDA+��BCE=![]() ����CAB+��CBA��=50���� ���DCE=130����
����CAB+��CBA��=50���� ���DCE=130����
(2)���ߡ�ACB=80���� ���A+��B=100���� ��AD=AC��BE=BC�� ���ACD=��ADC����BEC=��BCE��
���ADC=![]() ����BEC=
����BEC=![]() �� ���ADC+��BEC=180�㩁
�� ���ADC+��BEC=180�㩁![]() ����A+��B��=130�������DCE=50����
����A+��B��=130�������DCE=50����
(3)����D��E�ֱ���ֱ��AB�ϣ���ȥ��1����2��������������������������ͼ3��
�ɣ�1��֪����D=![]() CAB���ɣ�2��֪��CEB=
CAB���ɣ�2��֪��CEB=![]() �� ���CEB=��D+��DCE��
�� ���CEB=��D+��DCE��
��![]() =
=![]() CAB+��DCE�� ���DCE=40���� ��ͼ4��ͬ����DCE=40����
CAB+��DCE�� ���DCE=40���� ��ͼ4��ͬ����DCE=40����
(4)������ABC��AB=14��AC=15��BC=13�� ��C��CF��AB��F��
(5)��AC2��AF2=BC2��BF2����152��AF2=132����14��AF��2�� ��ã�AF=9�� ��CF=12��
����ͼ1��DE=AB+AC+BC=42�� ��S��CDE=![]() ��42��12=252��
��42��12=252��
����ͼ2��DE=AC+BC��AB=14�� ��S��CDE=![]() ��14��12=84��
��14��12=84��
����ͼ3��DE=AC+AB��BC=16�� ��S��CDE=![]() ��16��12=96��
��16��12=96��
����ͼ4��DE=AB+BC��AC=12�� ��S��CDE=![]() ��12��12=72��
��12��12=72��