题目内容
【题目】有这样一个问题:探究函数![]() 的性质.
的性质.
(1)先从简单情况开始探究:
① 当函数为![]() 时,
时, ![]() 随
随![]() 增大而 (填“增大”或“减小”);
增大而 (填“增大”或“减小”);
② 当函数为![]() 时,它的图象与直线
时,它的图象与直线![]() 的交点坐标为 ;
的交点坐标为 ;
(2)当函数为![]() 时,
时,
下表为其y与x的几组对应值.
x | … |
| 0 | 1 |
| 2 |
| 3 | 4 |
| … |
y | … |
|
| 1 |
| 2 |
| 3 | 7 |
| … |

①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质: .
【答案】(1)①增大;②(1,1),(2,2); (2)①图形见解析(3)性质见解析
【解析】试题分析:(1)①整理成一次函数的一般式,根据一次函数的性质得出即可;
②求出组成的方程组的解,即可得出答案;
(2)①把各个点用平滑的曲线连接即可;②根据图象和(1)中结论写出一个符合的信息即可.
试题分析 :
解:(1)①∵y=![]() (x-1)+x=
(x-1)+x=![]() x-
x-![]() ,
,
k=![]() >0,
>0,
∴y随x增大而增大,
故答案为:增大;
②解方程组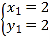
得: ![]() ,
, ![]() ,
,
所以两函数的交点坐标为(1,1),(2,2),
故答案为:(1,1),(2,2);
(2)①如图:
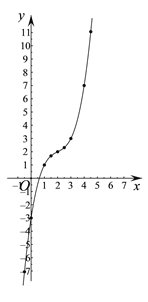
②该函数的性质:
a、y随x的增大而增大;
b、函数的图象经过第一、三、四象限;
c、函数的图象与x轴y轴各有一个交点;
d、函数图象与直线y=x的交点坐标为(1,1)(2,2)(3,3).

练习册系列答案
相关题目