题目内容
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD.若AD=4,BC=6,则梯形ABCD的面积是 . 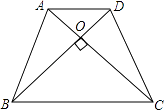
【答案】25
【解析】解:过点D作DE∥AC,交BC的延长线于点E, 
∵AD∥BC,
∴四边形ACED是平行四边形,
∴AC=DE,CE=AD=4,
∴BE=BC+CE=6+4=10,
∵AC⊥BD,
∴DE⊥BD,
∵四边形ABCD是等腰梯形,
∴AC=BD,
∴BD=DE,
∴BD=DE= ![]() =5
=5 ![]() ,
,
∴S梯形ABCD= ![]() ×AC×BD=25.
×AC×BD=25.
所以答案是:25.
【考点精析】本题主要考查了等腰三角形的性质和等腰梯形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等才能正确解答此题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
【题目】为了从甲、乙两名射击运动员中选拔一名参加比赛,对这两名运动员进行测试,他们10次射击命中的环数如下:
甲 | 7 | 9 | 8 | 6 | 10 | 7 | 9 | 8 | 6 | 10 |
乙 | 7 | 8 | 9 | 8 | 8 | 6 | 8 | 9 | 7 | 10 |
根据测试成绩,你认为选择哪一名运动员参赛更好?为什么?
【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |

(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).