题目内容
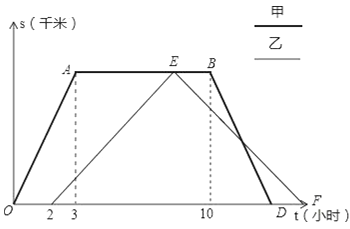
【题目】甲乙两车从姜堰去往扬州市，甲比乙早出发了2个小时，甲到达扬州市后停留一段时间返回，乙到达扬州市后立即返回．甲车往返的速度都为80千米/时，乙车往返的速度都为40千米/时，下图是两车距姜堰的路程S（千米）与行驶时间t（小时）之间的函数图象．请结合图象回答下列问题：
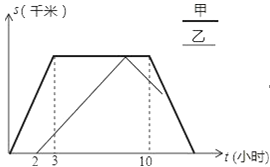
（1）姜堰、扬州两地的距离是 千米；甲到扬州市后， 小时乙到达扬州市；
（2）求甲车返回时的路程S（千米）与时间t（小时）之间的函数关系式，并写出自变量t的取值范围；
（3）求甲车从扬州市往回返后再经过几小时两车相距30千米．
【答案】（1）120；5；（2）S1=-40t+520．t的取值范围为：10≤t≤13；（3）3.5小时或0.5小时或2.5小时.
【解析】
试题分析：（1）根据路程=速度×时间的数量关系用甲车的速度×甲车到达乙地的时间就可以求出两地的距离，根据时间=路程÷速度就可以求出乙需要的时间；
（2）由（1）的结论可以求出BD的解析式，由待定系数法就可以求出结论；
（3）运用待定系数法求出EF的解析式，再由两车之间的距离公式建立方程求出其解即可．
试题解析：（1）由题意，得
40×3=120km．
120÷20-3+2=5小时，
（2）∵姜堰、扬州两地的距离是120km，
∴A（3，120），B（10，120），D（13，0）．
设线段BD的解析式为S1=k1t+b1，由题意，得．
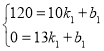
解得：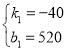
，
∴S1=-40t+520．t的取值范围为：10≤t≤13；
（3）设EF的解析式为s2=k2t+b2，由题意，得
，
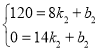解得：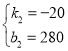
，
S2=-20t+280．
当-20t+280-（-40t+520）=30时，
t=13.5；
∴13.5-10=3.5（小时），
当-40t+520-（-20t+280）=30时，
t=10.5，
∴10.5-10=0.5（小时），
当120-20（t-8）=30时，
t=12.5，
∴12.5-10=2.5（小时），
答：甲车从B市往回返后再经过3.5小时或0.5小时或2.5两车相距30千米．
