题目内容
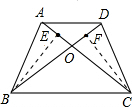
如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,点E、F分别在线段AO、DO上,且AE=DF,则四边形BEFC是______.


∵四边形ABCD是梯形,AD∥BC,AB=CD,
∴AC=DB,∠BAD=∠CDA,
又∵AD=DA,AB=CD,
∴△BAD≌△CDA,
∴∠OAD=∠ODA,
∴OA=OD,
∵AE=DF,
∴OA-AE=OD-DF,
即OE=OF,
∴
=
,
∴EF∥AD,
∴EF∥BC,
又∵BE不平行CF,
∴四边形BEFC是梯形,
∵AC=DB,AE=DF,
∴AC-AE=DB-DF,
即EC=FB,
∴梯形BEFC是等腰梯形.
∴AC=DB,∠BAD=∠CDA,
又∵AD=DA,AB=CD,
∴△BAD≌△CDA,
∴∠OAD=∠ODA,
∴OA=OD,
∵AE=DF,
∴OA-AE=OD-DF,
即OE=OF,
∴
| OE |
| OA |
| OF |
| OD |
∴EF∥AD,
∴EF∥BC,
又∵BE不平行CF,
∴四边形BEFC是梯形,
∵AC=DB,AE=DF,
∴AC-AE=DB-DF,
即EC=FB,
∴梯形BEFC是等腰梯形.


练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
 与正方形
与正方形 的位置如图所示.
的位置如图所示.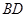 交
交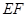 于点
于点 ;
;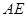 上取一点
上取一点 ,联结
,联结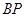 ,
,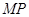 ,使△
,使△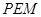 与△
与△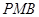 相似;
相似;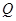 是线段
是线段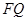 并延长交四边形
并延长交四边形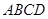 的一边于点
的一边于点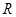 ,且满足
,且满足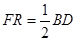 ,则
,则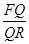 的值为_____________.
的值为_____________.