题目内容
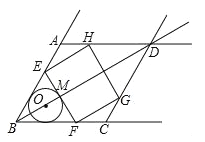
【题目】(2016浙江省温州市第24题)如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6![]() ,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
(1)求证:BO=2OM.
(2)设EF>HE,当矩形EFGH的面积为24![]() 时,求⊙O的半径.
时,求⊙O的半径.
(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.
【答案】(1)、答案见解析;(2)、2或4;(3)、18﹣6![]() 或9或18或18+6
或9或18或18+6![]() .
.
【解析】
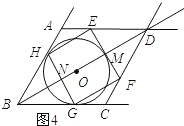
试题分析:(1)、设⊙O切AB于点P,连接OP,由切线的性质可知∠OPB=90°.先由菱形的性质求得∠OBP的度数,然后依据含30°直角三角形的性质证明即可;(2)、设GH交BD于点N,连接AC,交BD于点Q.先依据特殊锐角三角函数值求得BD的长,设⊙O的半径为r,则OB=2r,MB=3r.当点E在AB上时.在Rt△BEM中,依据特殊锐角三角函数值可得到EM的长(用含r的式子表示),由图形的对称性可得到EF、ND、BM的长(用含r的式子表示,从而得到MN=18﹣6r,接下来依据矩形的面积列方程求解即可;当点E在AD边上时.BM=3r,则MD=18﹣3r,最后由MB=3r=12列方程求解即可;(3)、先根据题意画出符合题意的图形,①如图4所示,点E在AD上时,可求得DM=![]() r,BM=3r,然后依据BM+MD=18,列方程求解即可;②如图5所示;依据图形的对称性可知得到OB=
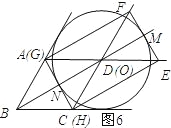
r,BM=3r,然后依据BM+MD=18,列方程求解即可;②如图5所示;依据图形的对称性可知得到OB=![]() BD;③如图6所示,可证明D与O重合,从而可求得OB的长;④如图7所示:先求得DM=
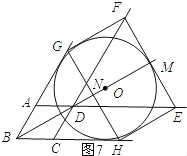
BD;③如图6所示,可证明D与O重合,从而可求得OB的长;④如图7所示:先求得DM=![]() r,OMB=3r,由BM﹣DM=DB列方程求解即可.
r,OMB=3r,由BM﹣DM=DB列方程求解即可.
试题解析:(1)、如图1所示:设⊙O切AB于点P,连接OP,则∠OPB=90°. ∵四边形ABCD为菱形,
∴∠ABD=![]() ∠ABC=30°.∴OB=2OP. ∵OP=OM, ∴BO=2OP=2OM.
∠ABC=30°.∴OB=2OP. ∵OP=OM, ∴BO=2OP=2OM.
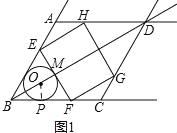
(2)、如图2所示:设GH交BD于点N,连接AC,交BD于点Q. ∵四边形ABCD是菱形,
∴AC⊥BD. ∴BD=2BQ=2ABcos∠ABQ=![]() AB=18. 设⊙O的半径为r,则OB=2r,MB=3r.
AB=18. 设⊙O的半径为r,则OB=2r,MB=3r.
∵EF>HE, ∴点E,F,G,H均在菱形的边上.
①如图2所示,当点E在AB上时.
在Rt△BEM中,EM=BMtan∠EBM=![]() r. 由对称性得:EF=2EM=2
r. 由对称性得:EF=2EM=2![]() r,ND=BM=3r.
r,ND=BM=3r.
∴MN=18﹣6r. ∴S矩形EFGH=EFMN=2![]() r(18﹣6r)=24
r(18﹣6r)=24![]() . 解得:r1=1,r2=2.
. 解得:r1=1,r2=2.
当r=1时,EF<HE, ∴r=1时,不合题意舍 当r=2时,EF>HE, ∴⊙O的半径为2. ∴BM=3r=6.
如图3所示: 当点E在AD边上时.BM=3r,则MD=18﹣3r. 由对称性可知:NB=MD=6.
∴MB=3r=18﹣6=12. 解得:r=4. 综上所述,⊙O的半径为2或4.
(3)、解设GH交BD于点N,⊙O的半径为r,则BO=2r.
当点E在边BA上时,显然不存在HE或HG与⊙O相切.
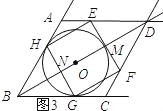
①如图4所示,点E在AD上时. ∵HE与⊙O相切, ∴ME=r,DM=![]() r. ∴3r+
r. ∴3r+![]() r=18.
r=18.
解得:r=9﹣3![]() . ∴OB=18﹣6
. ∴OB=18﹣6![]() .
.
②如图5所示;由图形的对称性得:ON=OM,BN=DM. ∴OB=![]() BD=9.
BD=9.
③如图6所示.∵HG与⊙O相切时,MN=2r.∵BN+MN=BM=3r. ∴BN=r. ∴DM=![]() FM=
FM=![]() GN=BN=r.
GN=BN=r.
∴D与O重合. ∴BO=BD=18.
④如图7所示:∵HE与⊙O相切,∴EM=r,DM=![]() r.∴3r﹣
r.∴3r﹣![]() r=18. ∴r=9+3
r=18. ∴r=9+3![]() .
.
∴OB=2r=18+6![]() .
.
综上所述,当HE或GH与⊙O相切时,OB的长为18﹣6![]() 或9或18或18+6
或9或18或18+6![]() .
.



 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案