题目内容
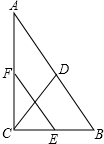
如图,△ABC中,BD为AC边上的中线,BE平分∠CBD,AF⊥BE,分别交BC、BE、BD于F、G、H.
(1)求证:CF=2DH;
(2)若AB=BC,cos∠BCA=
,DE=4,求HD的长.

(1)求证:CF=2DH;
(2)若AB=BC,cos∠BCA=
| 3 |
| 5 |

(1)证明:取AF的中点M,连接MD,
∵AD=DC,
∴CF=2MD,且MD∥BC,
∴∠DMH=∠BFH,
又∵∠BGH=∠BGF=90°,∠HBG=∠FBG,
∴∠BHG=∠BFH,
而∠DMH=∠BFH,∠DHM=∠BHG,
∴∠DMH=∠DHM,
∴DH=DM.而CF=2MD,
∴CF=2DH;
(2)过E作EN⊥BC于N,
∵AB=BC,AD=DC,
∴BD⊥AC,而BE平分∠CBD,EN⊥BC,
∴EN=DE=4,
在Rt△CEN中,cos∠BCA=
=
,
∴设CN=3k,则CE=5k,得EN=4k=4.
∴k=1,CE=5,CD=9,
在Rt△BCD中,cos∠BCA=
=
,
∴BC=15,BD=12,
又∵∠BHG=∠BFH,
∴BH=BF,
设DH=x,则FC=2x,BH=12-x,BF=15-2x.
由12-x=15-2x,得x=3,
∴HD=3.
∵AD=DC,
∴CF=2MD,且MD∥BC,
∴∠DMH=∠BFH,
又∵∠BGH=∠BGF=90°,∠HBG=∠FBG,
∴∠BHG=∠BFH,
而∠DMH=∠BFH,∠DHM=∠BHG,
∴∠DMH=∠DHM,
∴DH=DM.而CF=2MD,
∴CF=2DH;

(2)过E作EN⊥BC于N,
∵AB=BC,AD=DC,
∴BD⊥AC,而BE平分∠CBD,EN⊥BC,
∴EN=DE=4,
在Rt△CEN中,cos∠BCA=
| CN |
| CE |
| 3 |
| 5 |
∴设CN=3k,则CE=5k,得EN=4k=4.
∴k=1,CE=5,CD=9,
在Rt△BCD中,cos∠BCA=
| CD |
| BC |
| 3 |
| 5 |
∴BC=15,BD=12,
又∵∠BHG=∠BFH,
∴BH=BF,
设DH=x,则FC=2x,BH=12-x,BF=15-2x.
由12-x=15-2x,得x=3,
∴HD=3.

练习册系列答案
相关题目