题目内容
【题目】已知:二次函数y=﹣x2+![]() x+c与x轴交于点M(x1,0)N(x2,0)两点,与y轴交于点H.
x+c与x轴交于点M(x1,0)N(x2,0)两点,与y轴交于点H.
(1)若∠HMO=45°,∠MHN=105°时,求函数解析式;
(2)若|x1|2+|x2|2=1,当点Q(b,c)在直线![]() 上时,求二次函数y=﹣x2+
上时,求二次函数y=﹣x2+![]() x+c的解析式.
x+c的解析式.

【答案】(1)y=﹣x2+(1﹣![]() )x+
)x+![]() ;(2)y=﹣x2+
;(2)y=﹣x2+![]() x+
x+![]() .
.
【解析】
(1)由已知可得两个特殊的直角三角形,其公共直角边OH=c,解直角三角形得OM,ON的长度,用长度表示点M、N的横坐标,用两根关系求待定系数,即可确定二次函数关系式;
(2)由(1)可知x1=﹣c,x2=![]() c,代入已知条件,用待定系数法解答即可.
c,代入已知条件,用待定系数法解答即可.
(1)依题意得:OH=c,∠OHN=60°,解直角三角形得:OM=OH=c,ON=![]() c,即M(﹣c,0),N(
c,即M(﹣c,0),N(![]() c,0),∴﹣c+
c,0),∴﹣c+![]() c=
c=![]() ,﹣c
,﹣c![]() c=﹣c,解得:b=3﹣
c=﹣c,解得:b=3﹣![]() ,c=
,c=![]() ,故函数解析式y=﹣x2+(1﹣
,故函数解析式y=﹣x2+(1﹣![]() )x+
)x+![]() ;
;
(2)由|x1|2+|x2|2=1得:(x1+x2)2﹣2x1x2=1,∴![]() +2c=1…①.
+2c=1…①.
又∵点Q(b,c)在直线![]() 上,∴c=
上,∴c=![]() +
+![]() …②,由①②得:
…②,由①②得: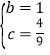 或
或![]() (不合题意舍去),∴二次函数y=﹣x2+
(不合题意舍去),∴二次函数y=﹣x2+![]() x+c的解析式y=﹣x2+
x+c的解析式y=﹣x2+![]() x+
x+![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目