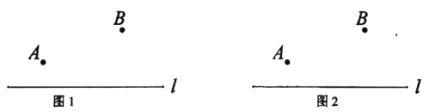题目内容
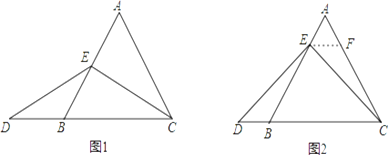
【题目】如图1, △ABC和△CDE均为等腰三角形,AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a,且点A、D、E在同一直线上,连结BE.

(1)求证: AD=BE.
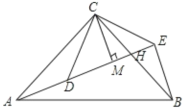
(2)如图2,若a=90°,CM⊥AE于E.若CM=7, BE=10, 试求AB的长.
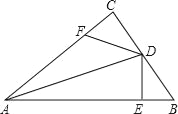
(3)如图3,若a=120°, CM⊥AE于E, BN⊥AE于N, BN=a, CM=b,直接写出AE的值(用a, b 的代数式表示).
【答案】(1)见解析;(2)26;(3)![]() +
+![]() b
b
【解析】
(1)由∠ACB=∠DCE可得出∠ACD=∠BCE,再利用SAS判定△ACD≌△BCE,即可得到AD=BE;
(2)由等腰直角三角形的性质可得CM=![]() DE,同(1)可证△ACD≌△BCE,得到AD=BE,然后可求AE的长,再判断∠AEB=90°,即可用勾股定理求出AB的长;
DE,同(1)可证△ACD≌△BCE,得到AD=BE,然后可求AE的长,再判断∠AEB=90°,即可用勾股定理求出AB的长;
(3)由等腰三角形的性质易得∠CAB=∠CBA=∠CDE=∠CED=30°,根据30度所对的直角边是斜边的一半可求出DE=2![]() CM,然后利用三角形外角性质推出∠BEN=60°,在Rt△BEN中即可求出BE,由于BE=AD,所以利用AE=AD+DE即可得出答案.
CM,然后利用三角形外角性质推出∠BEN=60°,在Rt△BEN中即可求出BE,由于BE=AD,所以利用AE=AD+DE即可得出答案.
证明:(1)∵∠ACB=∠DCE
∴∠ACB-∠BCD=∠DCE-∠BCD,即∠ACD=∠BCE
在△ACD和△BCE中,
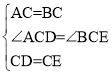
∴△ACD≌△BCE(SAS)
∴AD=BE
(2)∵∠DCE=90°,CD=CE,
∴△DCE为等腰直角三角形,
∵CM⊥DE,
∴CM平分DE,即M为DE的中点
∴CM=![]() DE,
DE,
∴DE=2CM=14,
∵∠ACB=∠DCE
∴∠ACB-∠BCD=∠DCE-∠BCD,即∠ACD=∠BCE
在△ACD和△BCE中,
∴△ACD≌△BCE(SAS)
∴AD=BE=10,∠CAD=∠CBE
∴AE=AD+DE=24
如图,设AE,BC交于点H,
在△ACH和△BEH中,
∠CAH+∠ACH=∠EBH+∠BEH,而∠CAH=∠EBH,
∴∠BEH=∠ACH=90°,
∴△ABE为直角三角形
由勾股定理得![]()
(3)由(1)(2)可得△ACD≌△BCE,
∴∠DAC=∠EBC,
∵△ACB,△DCE都是等腰三角形,∠ACB=∠DCE=120°
∴∠CAB=∠CBA=∠CDE=∠CED=30°,
∵CM⊥DE,
∴∠CMD=90°,DM=EM,
∴CD=CE=2CM,DM=EM=![]() CM
CM
∴DE=2![]() CM=2
CM=2![]() b
b
∵∠BEN=∠BAE+∠ABE=∠BAE+∠EBC+∠CBA=∠BAE+∠DAC+∠CBA=30°+30°=60°,
∴∠NBE=30°,
∴BE=2EN,BN=![]() EN
EN
∵BN=a
∴BE=2EN=![]() =AD
=AD
∴AE=AD+DE=![]()