Question

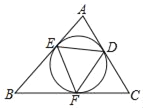
【题目】如图，△ABC的内切圆与三边分别相切于点D、E、F，则下列等式：

①∠EDF＝∠B；

②2∠EDF＝∠A＋∠C；

③2∠A＝∠FED＋∠EDF；

④∠AED＋∠BFE＋∠CDF＝180°，其中成立的个数是（　　）

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】B

【解析】

根据内接圆与圆的内接三角形的性质进行判断.

由题意可知AD＝AE，CD＝CF，∴∠ADE＝∠AED，∠CDF＝∠CFD，∴∠EDF＝180°－∠ADE－∠CDF＝180°－(180°－∠A)－(180°－∠C)＝∠A＋∠C，∴2∠EDF＝∠A＋∠C，②成立；易得∠AED＝(180°－∠A)，∠BFE＝(180°－∠B)，∠CDF＝(180°－∠C)，∴∠AED＋∠BFE＋∠CDF＝[180°×3－(∠A＋∠B＋∠C)]＝180°，∴④成立；若∠EDF＝∠B，则∠BEF＝∠B，∴＝∠B，∴∠B＝60°，与题中条件不不符，①不成立；若2∠A＝∠FED＋∠EDF，则2∠A＝∠FDC＋∠BEF，∴2∠A＝，∴2∠A＝，解得∠A＝60°，与题中条件不符，故③不成立.故选B.