题目内容
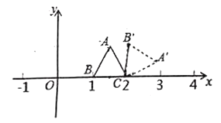
【题目】如图，在平面直角坐标系中，有一个正三角形
，其中
，
的坐标分别为
和
．若在无滑动的情况下，将这个正三角形沿着
轴向右滚动，则在滚动过程中，这个正三角形的顶点
，，中，会过点
的是点__________．
【答案】C
【解析】
先得到三角形的边长为1，再计算2020-2=2018，2018÷3=672……2，而672=224×3，即向右滚动672个60°后点A过点（2020，0），此时再绕A滚动60°点C过点（2020，1）．
∵C，B的坐标分别为（2，0）和（1，0），
∴三角形的边长为1，
∴三角形每向右滚动60°时，其中一个点的纵坐标为
，
∵2020-2=2018，
2018÷3=672，
而672=224×3，
∴点A过点（2020，0），
∴点C过点（2020，1）．
故答案为C．
练习册系列答案
相关题目
