题目内容
等腰直角三角形AOB中腰OA=OB=6,将它放在一个平面直角坐标系内,如图所示,已知点P是AB边上一动点,点Q是OA边上的定点,OQ=4.设点P的坐标是(x,y),△OPQ的面积为S.
(1)求y与x的函数关系式;
(2)求S与x的函数关系式,并求出当S=10时,点P的坐标.
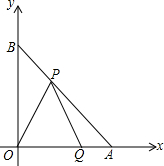
(1)求y与x的函数关系式;
(2)求S与x的函数关系式,并求出当S=10时,点P的坐标.

(1)作PC⊥x轴于点C,
∵点P(x,y),
∴OC=x,PC=y.∠PCA=90°,
∵△AOB是等腰直角三角形
∴∠OAB=45°即∠PAC=45°,
∴∠CPA=∠CAP=45°
∴PC=CA=y,
∵OA+CA=6即x+y=6,
∴y与x的函数关系式为y=6-x(0<x<6);
(2)∵S=
OQ•PC=
×4×y=
×4×(6-x)=12-2x,
∴当S=10时,即10=12-2x,解得x=1,此时y=6-1=5,
∴此时点P的坐标为(1,5).
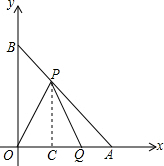
∵点P(x,y),
∴OC=x,PC=y.∠PCA=90°,
∵△AOB是等腰直角三角形
∴∠OAB=45°即∠PAC=45°,
∴∠CPA=∠CAP=45°
∴PC=CA=y,
∵OA+CA=6即x+y=6,
∴y与x的函数关系式为y=6-x(0<x<6);
(2)∵S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当S=10时,即10=12-2x,解得x=1,此时y=6-1=5,
∴此时点P的坐标为(1,5).


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

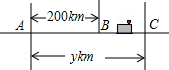
 系的图象如图.根据图象解决下列问题:
系的图象如图.根据图象解决下列问题:
