题目内容
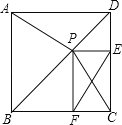
【题目】如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
(1)求证:△APD≌△CPD;
(2)若CF=3,CE=4,求AP的长.
【答案】(1)证明见解析;(2)5.
【解析】试题分析:
(1)根据正方形的性质,用SAS证明△APD≌△CPD;
(2)证明四边形PEDF是矩形,用勾股定理求EF,结合矩形的性质和(1)的结论求AP的长.
试题解析:
证明:(1)∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP=45°,∠BCD=90°,
在△APD和△CPD中,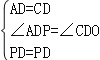 ,
,
∴△APD≌△CPD(SAS);
(2)解:∵△APD≌△CPD,∴AP=PC,
∵四边形ABCD是正方形,∴∠BCD=90°,
∵PE⊥DC,PF⊥BC,∴∠PEC=∠PFC=90°,
∴四边形PECF是矩形,∴PC=EF,∴AP=EF.
∵∠DCB=90°,∴在Rt△CEF中,EF=![]() =
=![]() =5,
=5,
∴AP=EF=5.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目