题目内容
【题目】如图,直线y=-x+1和直线y=x-2相交于点P,分别与y轴交于A、B两点.
(1)求点P的坐标;
(2)求△ABP的面积;
(3)M、N分别是直线y=-x+1和y=x-2上的两个动点,且MN∥y轴,若MN=5,直接写出M、N两点的坐标.

【答案】(1)P点坐标为![]() ;(2)
;(2)![]() ;(3)M(4,-3) ,N(4,2) 或M(-1,2) ,N(-1,-3)
;(3)M(4,-3) ,N(4,2) 或M(-1,2) ,N(-1,-3)
【解析】
(1)通过两条直线方程联立成一个方程组,解方程组即可得到点P的坐标;
(2)利用三角形面积公式![]() 解题即可;
解题即可;
(3)分别设出M,N的坐标,利用MN=5建立方程求解即可.
解:(1)∵直线y=-x+1和直线y=x-2相交于点P
∴![]() 解之得:
解之得: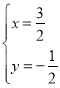
∴P点坐标为:![]()
(2)过P点作PD⊥y轴于点D
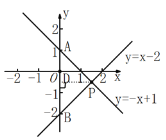
∵直线y=-x+1和直线y=x-2分别交y轴于A、B两点
当x=0时,![]()
∴A(0,1),B(0,-2)
∴![]()
∴ ![]()
由(1)知P![]()
∴![]()
![]()
(3)∵M、N分别是直线y=-x+1和y=x-2上的两个动点,MN∥y轴,
∴M,N的横坐标相同
设![]()
∵MN=5,
![]()
解得![]() 或
或![]()
当![]() 时,
时,![]() ,此时M(-1,2),N(-1,-3)
,此时M(-1,2),N(-1,-3)
当![]() 时,
时,![]() ,此时M(4,-3),N(4,2)
,此时M(4,-3),N(4,2)
综上所述,M(4,-3) ,N(4,2) 或M(-1,2) ,N(-1,-3)

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目