题目内容
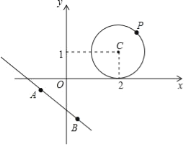
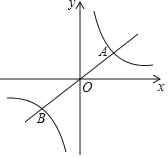
【题目】如图，反比例函数y＝
(k＞0)的图象与一次函数y＝
x的图象交于A、B两点(点A在第一象限)．若点A的横坐标为4．
(1)求k的值．
(2)根据图象，直接写出当＞x时，x的取值范围.
【答案】(1)12；(2)x＜﹣4或0＜x＜4．
【解析】
（1）先将x＝4代入正比例函数y＝
x，可得出y＝3，求得点A（4，3），再根据点A与B关于原点对称，得出B点坐标，求出k的值；
（2）正比例函数的值小于反比例函数的值即正比例函数的图象在反比例函数的图象下方，根据图象写出x的取值范围即可．
解：(1)∵点A在一次函数y＝x的图象上，
∴把x＝4代入正比例函数y＝x，
解得y＝3，∴点A(4，3)，
∵点A与B关于原点对称，
∴B点坐标为(﹣4，﹣3)，
把点A(4，3)代入反比例函数可得k=12；
(2)由交点坐标，根据图象可得当
＞x时，x的取值范围为：x＜﹣4或0＜x＜4．
练习册系列答案
相关题目
【题目】某电子厂商设计了一款制造成本为18元新型电子厂品，投放市场进行试销．经过调查，得到每月销售量y（万件）与销售单价x（元）之间的部分数据如下：
销售单价x（元/件） | … | 20 | 25 | 30 | 35 | … |
每月销售量y（万件） | … | 60 | 50 | 40 | 30 | … |
（1）求出每月销售量y（万件）与销售单价x（元）之间的函数关系式．
（2）求出每月的利润z（万元）与销售单x（元）之间的函数关系式．
（3）根据相关部门规定，这种电子产品的销售利润率不能高于50%，而且该电子厂制造出这种产品每月的制造成本不能超过900万元．那么并求出当销售单价定为多少元时，厂商每月能获得最大利润？最大利润是多少？（利润=售价﹣制造成本）
