题目内容
(1)如图1,在 ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
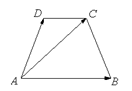
(2)如图2,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.
 ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.
ABCD中,点E,F分别在AB,CD上,AE=CF.求证:DE=BF.(2)如图2,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.

(1)证明见解析(2)75°
(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,
在△ADE和△CBF中,AD="CB" ,∠A=∠C ,AE=CF,
∴△ADE≌△CBF(SAS)。∴DE=BF;
(2)解:∵AB=AC,∠A=40°,∴∠ABC=∠C=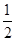 (180°-40°)=70°,
(180°-40°)=70°,
又∵BD是∠ABC的平分线,∴∠DBC=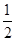 ∠ABC=35°。
∠ABC=35°。
∴∠BDC=180°-∠DBC-∠C=75°。
(1)根据四边形ABCD是平行四边形,利用平行四边形的性质得到一对边和一对角的对应相等,
在加上已知的一对边的相等,由“SAS”,证得△ADE≌△CBF,最后根据全等三角形的对应边相等即可得
证。
(2)根据AB=AC,利用等角对等边和已知的∠A的度数求出∠ABC和∠C的度数,再根据已知
的BD是∠ABC的平分线,利用角平分线的定义求出∠DBC的度数,最后根据三角形的内角和定理即可求出∠BDC的度数。
在△ADE和△CBF中,AD="CB" ,∠A=∠C ,AE=CF,
∴△ADE≌△CBF(SAS)。∴DE=BF;
(2)解:∵AB=AC,∠A=40°,∴∠ABC=∠C=
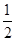 (180°-40°)=70°,
(180°-40°)=70°,又∵BD是∠ABC的平分线,∴∠DBC=
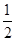 ∠ABC=35°。
∠ABC=35°。∴∠BDC=180°-∠DBC-∠C=75°。
(1)根据四边形ABCD是平行四边形,利用平行四边形的性质得到一对边和一对角的对应相等,
在加上已知的一对边的相等,由“SAS”,证得△ADE≌△CBF,最后根据全等三角形的对应边相等即可得
证。
(2)根据AB=AC,利用等角对等边和已知的∠A的度数求出∠ABC和∠C的度数,再根据已知
的BD是∠ABC的平分线,利用角平分线的定义求出∠DBC的度数,最后根据三角形的内角和定理即可求出∠BDC的度数。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案
相关题目


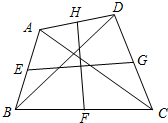

 中,
中, ∥
∥ ,
, ,
,
 ,
,
 ,请用向量
,请用向量 表示向量
表示向量
 .
.