题目内容
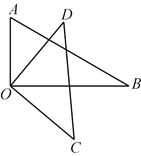
【题目】如图,将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)判断大小关系:∠AOD______∠BOC(填>、=、<等)
(2)若 ∠BOD=35°,则∠AOC= ;若∠AOC=135°,则∠BOD= ;
(3)猜想 ∠AOC与∠BOD的数量关系,并说明理由.
【答案】(1)、=;(2)、145°、45°;(3)猜想:∠AOC+∠BOD=180°,理由见解析.
【解析】
(1)由于是两直角三角形板重叠,∠AOD=90°-∠BOD,∠BOC=90°-∠BOD,即可判断∠AOD=∠BOC;
(2)由于是两直角三角形板重叠,根据∠AOC=∠AOB+∠COD-∠BOD可分别计算出∠AOC、∠BOD的度数;
(3)由∠AOD+∠BOD+∠BOD+∠BOC=180°且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补.
(1) ∵∠AOB=∠COD=90°,
∴∠AOD=90°-∠BOD,∠BOC=90°-∠BOD,
∴∠AOD=∠BOC;
(2)∵∠AOB=∠COD=90°,∠BOD=35°,
∴∠AOC=∠AOB+∠COD∠BOD=90°+90°35°=145°;
∵∠AOB=∠COD=90°,∠AOC=135°,
∴∠BOD=∠AOB+∠COD∠AOC=90°+90°135°=45°;
(3)、猜想:∠AOC+∠BOD=180°
理由: 依题意∠AOB=∠DOC=90°
∴∠AOC+∠BOD=(∠AOB+∠BOC)+∠BOD
=∠AOB+(∠BOC+∠BOD)
=∠AOB+∠DOC
=90°+90°
=180°.

【题目】某校举行了“文明在我身边”摄影比赛.已知每幅参赛作品成绩记为x分(60≤x<100).校方从600幅参赛作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制了如下不完整的统计图表.
分数段 | 频数 | 频率 |
60≤x<70 | 18 | 0.36 |
70≤x<80 | 17 | c |
80≤x<90 | a | 0.24 |
90≤x<100 | b | 0.06 |
合计 | 1 |

根据以上信息解答下列问题:
(1)统计表中c的值为________;样本成绩的中位数落在分数段________中;
(2)补全频数直方图;
(3)若80分以上(含80分)的作品将被组织展评,试估计全校被展评的作品数量是多少.