题目内容
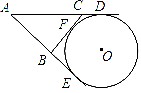
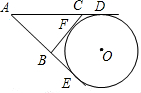 如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为
如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为
- A.20
- B.30
- C.40
- D.50
C
分析:根据切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,将△ABC的周长转化为切线长求解.
解答:据切线长定理有AD=AE,BE=BF,CD=CF;
则△ABC的周长=AB+BC+AC
=AB+BF+CF+AC
=AB+BE+AC+CD
=AD+AE=2AD
=40.
故选C.
点评:本题考查的是切线长定理,切线长定理图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.
分析:根据切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,将△ABC的周长转化为切线长求解.
解答:据切线长定理有AD=AE,BE=BF,CD=CF;
则△ABC的周长=AB+BC+AC
=AB+BF+CF+AC
=AB+BE+AC+CD
=AD+AE=2AD
=40.
故选C.
点评:本题考查的是切线长定理,切线长定理图提供了很多等线段,分析图形时关键是要仔细探索,找出图形的各对相等切线长.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 22、如图,已知AD和BC交于点O,且△OAB和△OCD均为等边三角形,以OD和OB为边作平行四边形ODEB,连接AC、AE和CE,CE和AD相交于点F.
22、如图,已知AD和BC交于点O,且△OAB和△OCD均为等边三角形,以OD和OB为边作平行四边形ODEB,连接AC、AE和CE,CE和AD相交于点F. 9、如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为( )
9、如图,AE、AD和BC分别切⊙O于点E、D、F,如果AD=20,则△ABC的周长为( )