题目内容
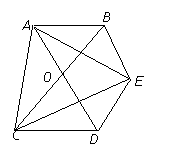
 22、如图,已知AD和BC交于点O,且△OAB和△OCD均为等边三角形,以OD和OB为边作平行四边形ODEB,连接AC、AE和CE,CE和AD相交于点F.
22、如图,已知AD和BC交于点O,且△OAB和△OCD均为等边三角形,以OD和OB为边作平行四边形ODEB,连接AC、AE和CE,CE和AD相交于点F.求证:△ACE为等边三角形.
分析:要证△ACE为等边三角形,可证有一个角为60°的等腰三角形是等边三角形,AE=CE可由△ABE≌△EDC得出,∠AEC=60°可由△CFD和△ADF中得出,从而命题可证.
解答:证明:∵△OAB和△OCD为等边三角形,
∴CD=OD,OB=AB,∠ADC=∠ABO=60°.
∵四边形ODEB是平行四边形,
∴OD=BE,OB=DE,∠CBE=∠EDO.
∴CD=BE,AB=DE,∠ABE=∠CDE.
∴△ABE≌△EDC.
∴AE=CE,∠AEB=∠ECD.
∵BE∥AD,
∴∠AEB=∠EAD.
∴∠EAD=∠ECD.
在△AFE和△CFD中
又∵∠AFE=∠CFD,
∴∠AEC=∠ADC=60°.
∴△ACE为等边三角形.
∴CD=OD,OB=AB,∠ADC=∠ABO=60°.
∵四边形ODEB是平行四边形,
∴OD=BE,OB=DE,∠CBE=∠EDO.
∴CD=BE,AB=DE,∠ABE=∠CDE.
∴△ABE≌△EDC.
∴AE=CE,∠AEB=∠ECD.
∵BE∥AD,
∴∠AEB=∠EAD.
∴∠EAD=∠ECD.
在△AFE和△CFD中
又∵∠AFE=∠CFD,
∴∠AEC=∠ADC=60°.
∴△ACE为等边三角形.
点评:本题综合考查考查等边三角形形的判定及性质,全等三角形平行四边形的有关知识.注意对三角形全等,等边三角形的综合应用.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,已知AD和BC交于点O,且△OAB和△OCD均为等边三角形,以OD和OB为边作平行四边形ODEB,连接AC、AE和CE,CE和AD相交于点F.
如图,已知AD和BC交于点O,且△OAB和△OCD均为等边三角形,以OD和OB为边作平行四边形ODEB,连接AC、AE和CE,CE和AD相交于点F.