题目内容
观察下面的表格:| x | 1 | 2 | |
| ax2 | 2 | ||
| ax2+bx+c | 4 | 6 |
(Ⅱ)求二次函数y=ax2+bx+c图象的顶点坐标与对称轴.
【答案】分析:(Ⅰ)把(1,2)点代入y=ax2中可以得到a的值,再分别把点A(0,4)和点B(2,6),代入二次函数y=x2+bx+c中得b=-3,c=4,求得二次函数的解析式;
(Ⅱ)根据二次函数图象的顶点坐标公式(-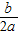 ,
,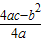 )代入数可以直接计算得到答案.
)代入数可以直接计算得到答案.
解答:解:(Ⅰ)∵x=1时,ax2=2,
∴a•12=2,
∴a=2,
∴y=2x2,
∴y=ax2+bx+c=2x2+bx+c,
∵当x=0时,y=4,当x=2时,y=6,
∴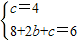 ,
,
解得: ;
;
如下表:
;
(Ⅱ)由(Ⅰ)得:y=2x2-3x+4,
∴顶点坐标是:(-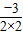 ,
,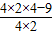 )
)
即:( ,
,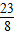 ).
).
对称轴为:x= .
.
点评:此题主要考查了待定系数法求二次函数解析式,以及求二次函数的顶点坐标,凡是函数图象经过的点,都能满足关系式,直接代入计算即可.
(Ⅱ)根据二次函数图象的顶点坐标公式(-
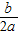 ,
,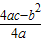 )代入数可以直接计算得到答案.
)代入数可以直接计算得到答案.解答:解:(Ⅰ)∵x=1时,ax2=2,
∴a•12=2,
∴a=2,
∴y=2x2,
∴y=ax2+bx+c=2x2+bx+c,
∵当x=0时,y=4,当x=2时,y=6,
∴
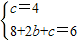 ,
,解得:
 ;
;如下表:
| x | 1 | 2 | |
| ax2 | 2 | 8 | |
| ax2+bx+c | 4 | 3 | 6 |
(Ⅱ)由(Ⅰ)得:y=2x2-3x+4,
∴顶点坐标是:(-
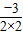 ,
,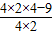 )
)即:(
 ,
,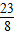 ).
).对称轴为:x=
 .
.点评:此题主要考查了待定系数法求二次函数解析式,以及求二次函数的顶点坐标,凡是函数图象经过的点,都能满足关系式,直接代入计算即可.

练习册系列答案
相关题目
探究发现:
解下列方程,将得到的解填入下面的表格中,观察表格中两个解的和与积,它们和原来的方程的系数有什么联系?
(1)x2-2x=0(2)x2+3x-4=0(3)x2-5x+6=0
| 方 程 | x1 | x2 | x1+x2 | x1•x2 |
| (1) | ||||
| (2) | ||||
| (3) |
(2)一般的,对于关于x的方程x2+px+q=0的两根为x1、x2,则x1+x2=______,x1•x2______.
(3)运用以上发现,解决下面的问题:
①已知一元二次方程x2-2x-7=0的两个根为x1,x2,则x1+x2的值为______
A.-2 B.2 C.-7 D.7
②已知x1,x2是方程x2-x-3=0的两根,试求(1+x1)(1+x2)和x12+x22的值.
解下列方程,将得到的解填入下面的表格中,观察表格中两个解的和与积,它们和原来的方程的系数有什么联系?
(1)x2-2x=0(2)x2+3x-4=0(3)x2-5x+6=0
| 方 程 | x1 | x2 | x1+x2 | x1.x2 |
| (1) | ______ | ______ | ______ | ______ |
| (2) | ______ | ______ | ______ | ______ |
| (3) | ______ | ______ | ______ | ______ |
一般的,对于关于x的方程x2+px+q=0(p,q为常数,p2-4q≥0)的两根为x1、x2
则x1+x2=______,x1.x2=______.
(2)运用以上发现,解决下面的问题:
①已知一元二次方程x2-2x-7=0的两个根为x1,x2,则x1+x2的值为______
A.-2 B.2 C.-7 D.7
②已知x1,x2是方程x2-x-3=0的两根,利用上述结论,不解方程,求x12+x22的值.
探究发现:
解下列方程,将得到的解填入下面的表格中,观察表格中两个解的和与积,它们和原来的方程的系数有什么联系?
(1)x2-2x=0(2)x2+3x-4=0(3)x2-5x+6=0
(1)请用文字语言概括你的发现.
(2)一般的,对于关于x的方程x2+px+q=0的两根为x1、x2,则x1+x2=______,x1•x2______.
(3)运用以上发现,解决下面的问题:
①已知一元二次方程x2-2x-7=0的两个根为x1,x2,则x1+x2的值为______
A.-2 B.2 C.-7 D.7
②已知x1,x2是方程x2-x-3=0的两根,试求(1+x1)(1+x2)和x12+x22的值.
解下列方程,将得到的解填入下面的表格中,观察表格中两个解的和与积,它们和原来的方程的系数有什么联系?
(1)x2-2x=0(2)x2+3x-4=0(3)x2-5x+6=0
| 方 程 | x1 | x2 | x1+x2 | x1•x2 |
| (1) | ||||
| (2) | ||||
| (3) |
(2)一般的,对于关于x的方程x2+px+q=0的两根为x1、x2,则x1+x2=______,x1•x2______.
(3)运用以上发现,解决下面的问题:
①已知一元二次方程x2-2x-7=0的两个根为x1,x2,则x1+x2的值为______
A.-2 B.2 C.-7 D.7
②已知x1,x2是方程x2-x-3=0的两根,试求(1+x1)(1+x2)和x12+x22的值.