Question

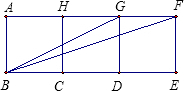
10、如图，已知3个边长相等的正方形相邻并排．则∠EBF+∠EBG=

45°

．

Answer 1

分析：根据题意将已知3个边长相等的正方形以BE为轴进行翻折，连接BG′，FG′设AB=a，再利用勾股定理即可解题．

解答：解：如图将已知3个边长相等的正方形
以BE为轴进行翻折，连接BG′，FG′，设AB=a
则有∠EBG=∠EBG′
∠EBG+∠EBF=∠EBG′+∠EBF=∠FBG′
又BG′²=a²+（2a）²=5a²
FG′²=a²+（2a）²=5a²，BF²=a²+（3a）²=10a²
所以BG′²+FG′²=BF²
∠FBG′=45°
∠EBG+∠EBF=45°．
故答案为：45°．

点评：本题主要考查了学生对相似三角形的判定与性质和勾股定理的理解和掌握，难度适中．