题目内容
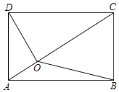
【题目】如图,正方形ABCD中,O是对角线AC、BD的交点,过点O作OE⊥OF,分别交AB、BC于E. F.

(1)求证:△OEF是等腰直角三角形。
(2)若AE=4,CF=3,求EF的长。
【答案】(1)见解析;(2)5.
【解析】
(1)根据正方形的性质可得∠ABO=∠ACF=45°,OB=OC,∠BOC=90°,再根据同角的余角相等求出∠EOB=∠FOC,然后利用“角边角”证明△BEO和△CFO全等,根据全等三角形对应边相等可得OE=OF,从而得证;
(2)根据全等三角形对应边相等可得BE=CF,再根据正方形的四条边都相等求出AE=BF,再利用勾股定理列式进行计算即可得解.
(1)证明:∵四边形ABCD为正方形,
∴∠ABO=∠ACF=45,OB=OC,∠BOC=90,
∴∠FOC+∠BOF=90,
又∵OE⊥OF,
∴∠EOF=90,
∴∠EOB+∠BOF=90,
∴∠EOB=∠FOC,
在△BEO和△CFO中,
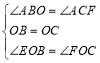 ,
,
∴△BEO≌△CFO(ASA),
∴OE=OF,
又∵∠EOF=90,
∴△DEF是等腰直角三角形;
(2)解∵△BEO≌△CFO(已证),
∴BE=CF=3,
又∵四边形ABCD是正方形,
∴AB=BC,
∴ABBE=BCCF,
即AE=BF=4,
在Rt△BEF中,EF=![]() =
=![]() =5.
=5.

练习册系列答案
相关题目