题目内容
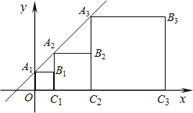
【题目】如图，在直角坐标系中，正方形A1B1C1O、 A2B2C2C1、A3B3C3C2、…、AnBnCnCn-1的顶点A1、A2、A3、…、An均在直线y＝kx＋b上，顶点C1、C2、C3、…、Cn在x轴上，若点B1的坐标为（1，1），点B2的坐标为（3，2），那么点A4的坐标为 ，点An的坐标为 ．
【答案】A4（7，8）；An（2n-1-1，2n-1）．
【解析】
∵点B1的坐标为（1，1），点B2的坐标为（3，2）
∴由题意知：A1的坐标是（0，1），A2的坐标是：（1，2），
∴直线A1A2的解析式是y=x+1．纵坐标比横坐标多1．
∵A1的纵坐标是：1=20，A1的横坐标是：0=20-1；
A2的纵坐标是：1+1=21，A2的横坐标是：1=21-1；
A3的纵坐标是：2+2=4=22，A3的横坐标是：1+2=3=22-1，
A4的纵坐标是：4+4=8=23，A4的横坐标是：1+2+4=7=23-1，即点A4的坐标为（7，8）．
∴An的纵坐标是：2n-1，横坐标是：2n-1-1，
即点An的坐标为（2n-1-1，2n-1）．
故答案为：（7，8）；（2n-1-1，2n-1）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某校七（1）班学生的平均身高是160厘米，下表给出了该班6名学生的身高情况（单位：厘米）.
学 生 | A | B | C | D | E | F |
身 高 | 157 | 162 | 159 | 154 | 163 | 165 |
身高与平均身高的差值 | －3 | ＋2 | －1 | a | ＋3 | b |
（1）列式计算表中的数据a和b；
（2）这6名学生中谁最高？谁最矮？最高与最矮学生的身高相差多少？
（3）这6名学生的平均身高与全班学生的平均身高相比，在数值上有什么关系？（通过计算回答）
