题目内容
(2010•鄂州)如图,在直角坐标系中,A(-1,0),B(0,2),一动点P沿过B点且垂直于AB的射线BM运动,P点的运动速度为每秒1个单位长度,射线BM与x轴交于点C.(1)求点C的坐标.
(2)求过点A、B、C三点的抛物线的解析式.
(3)若P点开始运动时,Q点也同时从C点出发,以P点相同的速度沿x轴负方向向点A运动,t秒后,以P、Q、C为顶点的三角形是等腰三角形.(点P到点C时停止运动,点Q也同时停止运动),求t的值.
(4)在(2)(3)的条件下,当CQ=CP时,求直线OP与抛物线的交点坐标.

【答案】分析:(1)由于AB⊥BC,则△AOB∽△BOC,由于OB=2OA,则OC=2OB,由此可求出C点的坐标.
(2)设抛物线方程为y=ax2+bx+c(a≠0),三点代入联立方程解出a、b、c.
(3)根据P、Q的速度,可用t表示出BP、CP、CQ的长,若以P、Q、C为顶点的三角形是等腰三角形,那么可分作三种情况考虑:
①CP=CQ,可联立CP、CQ的表达式,可得到关于t的等量关系式,即可求出此时t的值;
②CQ=QP,过Q作QM⊥BC于M,根据等腰三角形的性质知CM= CP,可通过△CQM∽△CBO所得比例线段,列出关于t的等量关系式,求出此时t的值;
CP,可通过△CQM∽△CBO所得比例线段,列出关于t的等量关系式,求出此时t的值;
③CP=PQ,过P作PN⊥OC于N,方法与②相同.
(4)在(2)题中已经求得CP=CQ时的t值,此时发现P是BC的中点,根据B、C的坐标,即可得到P点的坐标,易求得直线OP的解析式,联立抛物线的解析式可求出它与抛物线的交点坐标.
解答:解:(1)∵A(-1,0),B(0,2),
∴OA=1,OB=2,OB=2OA;
∵∠ABC=90°,易得△ABO∽△BCO,
∴AO:BO=BO:OC,即OC=2OB=4,
∴C(4,0).
(2)设抛物线方程为y=ax2+bx+c(a≠0),依题意有:
 ,
,
解得 ;
;
∴抛物线的解析式为y=- x2+
x2+ x+2.
x+2.
(3)∵OB=2,OC=4,
∴BC=2 ;
;
则:BP=t,CP=2 -t,CQ=t;
-t,CQ=t;
①CP=CQ,则有:2 -t=t,
-t=t,
解得:t= ;
;
②CQ=QP,过Q作QM′⊥BC于M′,则有:
CM′= (2
(2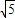 -t);
-t);
易证△CQM′∽△CBO,
则: =
= ,
,
即 ,
,
解得:t= =
= ;
;
③CP=PQ,过P作PN⊥OC于N,则:
CN= CQ=
CQ= t;
t;
易证△CNP∽△COB,则有: ,
,
即 ,
,
解得t= =
= ;
;
综上所述,当t=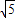 或
或 或
或 时,以P、Q、C为顶点的三角形是等腰三角形.
时,以P、Q、C为顶点的三角形是等腰三角形.
(4)由(3)知:当CP=CQ时,BP=t= =
= BC,即P是BC的中点,
BC,即P是BC的中点,
∵B(0,2),C(4,0),
∴P(2,1);
∴直线OP的解析式为:y= x;
x;
联立抛物线的解析式有:
 ,
,
解得 ,
, ;
;
∴直线OP与抛物线的交点为(1+ ,
, ),(1-
),(1- ,
, ).
).
点评:此题是二次函数的综合题,主要考查了相似三角形的性质、二次函数解析式的确定、函数图象交点坐标的求法以及等腰三角形的构成条件等重要知识,在等腰三角形腰和底不确定的情况下,一定要分类讨论,以免漏解.
(2)设抛物线方程为y=ax2+bx+c(a≠0),三点代入联立方程解出a、b、c.
(3)根据P、Q的速度,可用t表示出BP、CP、CQ的长,若以P、Q、C为顶点的三角形是等腰三角形,那么可分作三种情况考虑:
①CP=CQ,可联立CP、CQ的表达式,可得到关于t的等量关系式,即可求出此时t的值;
②CQ=QP,过Q作QM⊥BC于M,根据等腰三角形的性质知CM=
 CP,可通过△CQM∽△CBO所得比例线段,列出关于t的等量关系式,求出此时t的值;
CP,可通过△CQM∽△CBO所得比例线段,列出关于t的等量关系式,求出此时t的值;③CP=PQ,过P作PN⊥OC于N,方法与②相同.
(4)在(2)题中已经求得CP=CQ时的t值,此时发现P是BC的中点,根据B、C的坐标,即可得到P点的坐标,易求得直线OP的解析式,联立抛物线的解析式可求出它与抛物线的交点坐标.
解答:解:(1)∵A(-1,0),B(0,2),
∴OA=1,OB=2,OB=2OA;
∵∠ABC=90°,易得△ABO∽△BCO,
∴AO:BO=BO:OC,即OC=2OB=4,
∴C(4,0).
(2)设抛物线方程为y=ax2+bx+c(a≠0),依题意有:
 ,
,解得
 ;
;∴抛物线的解析式为y=-
 x2+
x2+ x+2.
x+2.(3)∵OB=2,OC=4,
∴BC=2
 ;
;则:BP=t,CP=2
 -t,CQ=t;
-t,CQ=t;①CP=CQ,则有:2
 -t=t,
-t=t,解得:t=
 ;
;②CQ=QP,过Q作QM′⊥BC于M′,则有:
CM′=
 (2
(2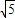 -t);
-t);易证△CQM′∽△CBO,
则:
 =
= ,
,即
 ,
,解得:t=
 =
= ;
;
③CP=PQ,过P作PN⊥OC于N,则:
CN=
 CQ=
CQ= t;
t;易证△CNP∽△COB,则有:
 ,
,即
 ,
,解得t=
 =
= ;
;综上所述,当t=
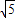 或
或 或
或 时,以P、Q、C为顶点的三角形是等腰三角形.
时,以P、Q、C为顶点的三角形是等腰三角形.(4)由(3)知:当CP=CQ时,BP=t=
 =
= BC,即P是BC的中点,
BC,即P是BC的中点,∵B(0,2),C(4,0),
∴P(2,1);
∴直线OP的解析式为:y=
 x;
x;联立抛物线的解析式有:
 ,
,解得
 ,
, ;
;∴直线OP与抛物线的交点为(1+
 ,
, ),(1-
),(1- ,
, ).
).点评:此题是二次函数的综合题,主要考查了相似三角形的性质、二次函数解析式的确定、函数图象交点坐标的求法以及等腰三角形的构成条件等重要知识,在等腰三角形腰和底不确定的情况下,一定要分类讨论,以免漏解.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

 ≈1.414,
≈1.414, ≈1.732,
≈1.732, ≈2.236)
≈2.236)
 +6
+6 ,则AB= .
,则AB= .
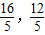 ),则点A1的坐标是( )
),则点A1的坐标是( )