题目内容
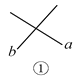
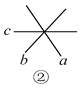
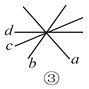
【题目】把一副三角板的直角顶点O重叠在一起,
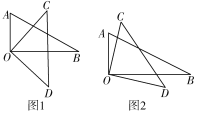
(1)如图1,当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
(2)如图2,当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
(3)当∠BOC的余角的4倍等于∠AOD时,则∠BOC是多少度?
【答案】(1)180°;(2)180°;(3)60°.
【解析】
试题(1)根据平分线的性质分别求出∠BOC和∠BOD的度数,然后求出∠AOD+∠BOC的度数;(2)、当不平分时可得∠AOD+∠BOC=∠AOB+∠COD求出答案;(3)结合前面两个可得∠AOD=180°-∠BOC=4(90°-∠BOC),求出∠BOC的度数.
试题解析:(1)当OB平分∠COD时,有∠BOC=∠BOD=45°,
于是∠AOC=90°-45°=45°,
∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°
(2)当OB不平分∠COD时,
有∠AOB=∠AOC+∠BOC=90°,∠COD=∠BOD+ ∠BOC=90°,
于是∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=∠AOB+∠COD,
∴∠AOD+∠BOC=90°+90°=180°.
(3)由上得∠AOD+∠BOC=180°,
有∠AOD=180°-∠BOC, 180°-∠BOC=4(90°-∠BOC),
∴∠BOC=60°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目