题目内容
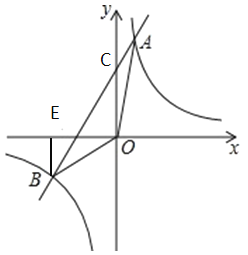
【题目】如图，在平面直角坐标系中抛物线
交
轴于点
，交
轴于点
，两点横坐标为
和
，点纵坐标为
．
求抛物线的解析式；
动点
在第四象限且在抛物线上，当
面积最大时，求点坐标，并求面积的最大值．
【答案】（1）y＝
x2﹣
x﹣4；（2）S有最大值
，D（
，﹣5）
【解析】
(1)根据抛物线与x轴的交点的横坐标为-1和3，可用交点式将此函数表示成y＝a（x+1）（x﹣3），再将它与y轴的交点（0，-4）代入这个解析式，求出a的值后即可得到此抛物线的解析式；（2）过D作垂直x轴的直线交BC于点N,这样可以将
分成
和
，利用
，在确定D点和N点的坐标后表示出DN的长，便能计算得到
，从而可以确定面积最大值，进而易求出点D的坐标．
解：（1）抛物线的表达式为：y＝a（x+1）（x﹣3）＝a（x2﹣2x﹣3），
将C（0，4）代入，
得﹣3a＝﹣4，解得：a＝，
∴抛物线的表达式为：y＝x2﹣x﹣4；
（2）过点D作y轴的平行线交BC于点N，
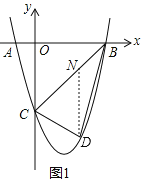
由B、C的坐标可得直线BC的表达式为：y＝
x﹣4，
设点D（x，x2﹣x﹣4），点N（x，x﹣4），
S△BCD＝
×OB×ND＝
3×（x﹣4﹣x2+x+4）＝﹣2x2+6x，
∵﹣2＜0，故S有最大值，
此时，x＝，点D（，﹣5）；
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
