题目内容
【题目】甲、乙两车从
地出发，沿同一条笔直的公路匀速驶向
地，乙车先到达地并停留
后，再以原速按原路返回，直至与甲车相遇.已知两车到地的距离
与甲车出发的时间
之间的函数关系分别如图中线段
和折线
所示，则图中点
的坐标为_______________.
【答案】
【解析】
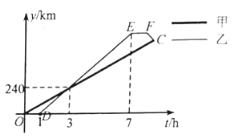
根据函数图象，先求出甲乙车的速度以及A，B两地之间的距离，进而求出乙从B地返回与甲相遇所花的时间，进而即可得到答案.
根据图象得：甲车的速度为：240÷3=80（km/h），乙车的速度为：240÷2=120（km/h），A，B两地之间的距离为：120×(7-1)=720（km），
乙从B地返回与甲相遇所花的时间为：(720-8×80)÷(80+120)=0.4（h），
此时，距A地的距离为：(8+0.4)×80=672（km），
∴点
的坐标为：．
练习册系列答案
相关题目
【题目】某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
销售单价（元） | x |
销售量y（件） |
|
销售玩具获得利润w（元） |
|
（2）在（1）问条件下，若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元．
（3）在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？
