��Ŀ����
��ͼ��Rt��OAC��һ�ŷ���ƽ��ֱ������ϵ�е�ֱ��������ֽƬ����O��ԭ���غϣ���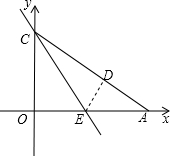 A��x���ϣ���C��y���ϣ�OC=
A��x���ϣ���C��y���ϣ�OC=| 3 |
��1�����ۺ�CE����ֱ�ߵĽ���ʽ��
��2�����D�����ꣻ
��3�����MΪֱ��CE�ϵ�һ�㣬����M��AC��ƽ���ߣ���y���ڵ�N���Ƿ���������ĵ�M��ʹ����M��N��D��CΪ������ı�����ƽ���ı��Σ������ڣ���������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��������1����Ϊ��CAO=30�㣬���۵���֪��OCE=��ECD=
��OCA=30�㣬
��Rt��COE�У��������Ǻ�������OE=OC•tan��OCE=
��
=1���Ӷ������E�������ǣ�1��0����
��ΪOC=
������C��0��
����
����ֱ��CE�Ľ���ʽΪy=kx+b����C��E��������룬�ɵõ�����k��b�ķ����飬��֮���ɣ�
��2����Rt��AOC�У��������Ǻ��������AC��AO��ֵ����ΪCD=OC=
�������AD=AC-CD=2
-
=
��
Ҫ��D�����꣬�����D��DF��OA�ڵ�F��
��Rt��AFD�У��������Ǻ�������DF=AD•sin��CAO=
��AF=AD•cos��CAO=
������OF=AO-AF=
���Ӷ���D�������ǣ�
��
����
��3�����������ۣ�
��һ����������˵��ڵ��������ڣ�������ΪM1���ӳ�DF��ֱ��CE��M1������M1O������DM1��y�ᣮ
��ΪOF=
�����Կ����M1������Ϊ��
��y1�������õ�M1��ֱ��CE�ϣ��ɵ�y1��ֵ�����������M1�������ǣ�
��-
����������DM1=DF+FM1=
+
=
��OC=
������DM1=OC��
����һ��Ա�ƽ������ȵ��ı�����ƽ���ı��ο�֪�ı���CDM1OΪƽ���ı��Σ�����O��y���ϣ����Ե�M1�Ƿ��������ĵ㣮
�ڶ���������˵��ڵڶ������ڣ���ΪM2���ɹ���D��DN��CE��y����N����N����NM2��CD��ֱ��CE�ڵ�M2�����ı���M2NDCΪƽ���ı��Σ�
����ƽ���ı��εĶԱ߷ֱ���ȣ���֪M2N=CD=
��
����M2N��CD��DN��CE�����ԡ�NM2C=��ACE����OCE=��M2CN��CN=M2N��
����M2N=CD=
������CN=
��
���ſ���M2H��y���ڵ�H��������ֱ��ƽ�У��ڴ�����ȿɵá�M2NC=��NCD�����M2NH=��OCA=60�㣮
��Rt��M2NH�У��������Ǻ��������M2H��NH��ֵ������HO=HN+CN+OC=
�ɵ�M2��-
��
����
| 1 |
| 2 |
��Rt��COE�У��������Ǻ�������OE=OC•tan��OCE=
| 3 |
| ||
| 3 |
��ΪOC=
| 3 |
| 3 |
����ֱ��CE�Ľ���ʽΪy=kx+b����C��E��������룬�ɵõ�����k��b�ķ����飬��֮���ɣ�
��2����Rt��AOC�У��������Ǻ��������AC��AO��ֵ����ΪCD=OC=
| 3 |
| 3 |
| 3 |
| 3 |
Ҫ��D�����꣬�����D��DF��OA�ڵ�F��
��Rt��AFD�У��������Ǻ�������DF=AD•sin��CAO=
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
��3�����������ۣ�
��һ����������˵��ڵ��������ڣ�������ΪM1���ӳ�DF��ֱ��CE��M1������M1O������DM1��y�ᣮ
��ΪOF=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
����һ��Ա�ƽ������ȵ��ı�����ƽ���ı��ο�֪�ı���CDM1OΪƽ���ı��Σ�����O��y���ϣ����Ե�M1�Ƿ��������ĵ㣮
�ڶ���������˵��ڵڶ������ڣ���ΪM2���ɹ���D��DN��CE��y����N����N����NM2��CD��ֱ��CE�ڵ�M2�����ı���M2NDCΪƽ���ı��Σ�
����ƽ���ı��εĶԱ߷ֱ���ȣ���֪M2N=CD=
| 3 |
����M2N��CD��DN��CE�����ԡ�NM2C=��ACE����OCE=��M2CN��CN=M2N��
����M2N=CD=
| 3 |
| 3 |
���ſ���M2H��y���ڵ�H��������ֱ��ƽ�У��ڴ�����ȿɵá�M2NC=��NCD�����M2NH=��OCA=60�㣮
��Rt��M2NH�У��������Ǻ��������M2H��NH��ֵ������HO=HN+CN+OC=
5
| ||
| 2 |
| 3 |
| 2 |
5
| ||
| 2 |
����⣺��1��������֪��CAO=30�㣬
���OCE=��ECD=
��OCA=30�㣬
����Rt��COE�У�OE=OC•tan��OCE=
��
=1��
���E�������ǣ�1��0����
��ֱ��CE�Ľ���ʽΪy=kx+b��
�ѵ�C��0��
����E��1��0�������
��
��
��
��ֱ��CE�Ľ���ʽΪy=-
x+
��
��2����Rt��AOC��AC=
=2
��
AO=
=3��
��CD=OC=
��
��AD=AC-CD=2
-
=
��
����D��DF��OA�ڵ�F��
��Rt��AFD�У�DF=AD•sin��CAO=
��
AF=AD•cos��CAO=
��
��OF=AO-AF=
��
���D�������ǣ�
��
����
��3��������������������M�㣬
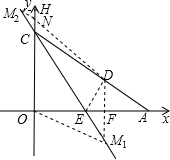 ��һ��������˵��ڵ��������ڣ���ΪM1���ӳ�DF��ֱ��CE��M1��
��һ��������˵��ڵ��������ڣ���ΪM1���ӳ�DF��ֱ��CE��M1��
����M1O��M1O��AC��
����DM1��y�ᣬ
��OF=
��
�����M1��������
��y1����
�֡ߵ�M1��ֱ��CE�ϣ�
�ཫ��M1���������y=-
x+
�У�
��y1=-
��
+
=-
����FM1=
��
���M1�������ǣ�
��-
����
�֡�DM1=DF+FM1=
+
=
��OC=
��
��DM1=OC��
�֡�DM1��OC��
���ı���CDM1OΪƽ���ı��Σ�
�֡ߵ�O��y���ϣ�
���M1�Ƿ��������ĵ㣮
�ڶ���������˵��ڵڶ������ڣ���ΪM2��
����D��DN��CE��y����N����N����NM2��CD��ֱ��CE�ڵ�M2��
���ı���M2NDCΪƽ���ı��Σ�
��M2N=CD=
��
��M2N��CD��DN��CE��
���NM2C=��ACE����OCE=��M2CN��
��CN=M2N��
��M2N=CD=
��
��CN=
��
��M2H��y���ڵ�H��
��M2N��CD��
���M2NC=��NCD��
���M2NH=��OCA=60�㣬
��Rt��M2NH��
M2H=M2N•sin60��=
��
=
��
NH=M2N•cos60��=
��
=
��
��HO=HN+CN+OC=
��
��M2��-
��
����
���M2�Ƿ��������ĵ㣬
�������������������������������ֱ�ΪM1��
��-
����M2��-
��
����
���OCE=��ECD=
| 1 |
| 2 |
����Rt��COE�У�OE=OC•tan��OCE=
| 3 |
| ||
| 3 |
���E�������ǣ�1��0����
��ֱ��CE�Ľ���ʽΪy=kx+b��
�ѵ�C��0��
| 3 |
|
��
|
��ֱ��CE�Ľ���ʽΪy=-
| 3 |
| 3 |
��2����Rt��AOC��AC=
| OC |
| sin��CAO |
| 3 |
AO=
| OC |
| tan��CAO |
��CD=OC=
| 3 |
��AD=AC-CD=2
| 3 |
| 3 |
| 3 |
����D��DF��OA�ڵ�F��
��Rt��AFD�У�DF=AD•sin��CAO=
| ||
| 2 |
AF=AD•cos��CAO=
| 3 |
| 2 |
��OF=AO-AF=
| 3 |
| 2 |
���D�������ǣ�
| 3 |
| 2 |
| ||
| 2 |
��3��������������������M�㣬
 ��һ��������˵��ڵ��������ڣ���ΪM1���ӳ�DF��ֱ��CE��M1��
��һ��������˵��ڵ��������ڣ���ΪM1���ӳ�DF��ֱ��CE��M1������M1O��M1O��AC��
����DM1��y�ᣬ
��OF=
| 3 |
| 2 |
�����M1��������
| 3 |
| 2 |
�֡ߵ�M1��ֱ��CE�ϣ�
�ཫ��M1���������y=-
| 3 |
| 3 |
��y1=-
| 3 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
���M1�������ǣ�
| 3 |
| 2 |
| ||
| 2 |
�֡�DM1=DF+FM1=
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
��DM1=OC��
�֡�DM1��OC��
���ı���CDM1OΪƽ���ı��Σ�
�֡ߵ�O��y���ϣ�
���M1�Ƿ��������ĵ㣮
�ڶ���������˵��ڵڶ������ڣ���ΪM2��
����D��DN��CE��y����N����N����NM2��CD��ֱ��CE�ڵ�M2��
���ı���M2NDCΪƽ���ı��Σ�
��M2N=CD=
| 3 |
��M2N��CD��DN��CE��
���NM2C=��ACE����OCE=��M2CN��
��CN=M2N��
��M2N=CD=
| 3 |
��CN=
| 3 |
��M2H��y���ڵ�H��
��M2N��CD��
���M2NC=��NCD��
���M2NH=��OCA=60�㣬
��Rt��M2NH��
M2H=M2N•sin60��=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
NH=M2N•cos60��=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
��HO=HN+CN+OC=
5
| ||
| 2 |
��M2��-
| 3 |
| 2 |
5
| ||
| 2 |
���M2�Ƿ��������ĵ㣬
�������������������������������ֱ�ΪM1��
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
5
| ||
| 2 |
����������Ľ����Ҫ�ۺ����ô���ϵ���������Ǻ�����֪ʶ���������������ⳣ�õ��������ۡ����ν�ϡ����̺�ת������ѧ˼�뷽����

��ϰ��ϵ�д�
 Сѧ��ʱ��ѵϵ�д�
Сѧ��ʱ��ѵϵ�д�
�����Ŀ
 �������ĵ�M��ʹ����M��N��D��CΪ������ı�����ƽ���ı��Σ������ڣ���������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
�������ĵ�M��ʹ����M��N��D��CΪ������ı�����ƽ���ı��Σ������ڣ���������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ� ��ͼ��Rt��OAC��һ�ŷ���ƽ��ֱ������ϵ�е�ֱ��������ֽƬ����O��ԭ���غϣ���A��x���ϣ���C��y���ϣ�OC=
��ͼ��Rt��OAC��һ�ŷ���ƽ��ֱ������ϵ�е�ֱ��������ֽƬ����O��ԭ���غϣ���A��x���ϣ���C��y���ϣ�OC= ����CAO=30°����Rt��OAC�۵���ʹOC������AC���ϣ���O���D�غϣ��ۺ�ΪCE��
����CAO=30°����Rt��OAC�۵���ʹOC������AC���ϣ���O���D�غϣ��ۺ�ΪCE��
 ����CAO=30�ȣ���Rt��OAC�۵���ʹOC������AC���ϣ���O���D�غϣ��ۺ�ΪCE��
����CAO=30�ȣ���Rt��OAC�۵���ʹOC������AC���ϣ���O���D�غϣ��ۺ�ΪCE��