题目内容
(2010•舟山模拟)如图,Rt△OAC是一张放在平面直角坐标系中的直角三角形纸片,点O与原点重合,点A在x轴上,点C在y轴上,OC= ,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.(1)求折痕CE所在直线的解析式;
(2)求点D的坐标.

【答案】分析:(1)由于∠ECO=∠DCE=30°,故有OE=OCtan30°=1,则点E(-1,0),再由待定系数法求得CE直线的解析式;
(2)过点D作DF⊥AO,则由三角函数的概念可求得EF、DF的值,从而得到点D的坐标.
解答:解:(1)由题意知,∠ACO=60°,OC= ,
,
∴∠ECO=∠DCE=30°,OE=OCtan30°=1
∴点E(-1,0),点C(0, )
)
设CE的解析式为y=kx+ ,
,
把点E的坐标代入得:0=-k+ ,
,
∴k= ,
,
∴CE的解析式为: ;(4分)
;(4分)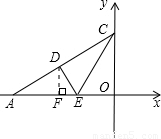
(2)过点D作DF⊥AO,
由题意知DE=OE=1,∠DEF=∠DEC=∠CEO=60°,
∴DF=DEsin∠DEF=1× =
= ,EF=DEcos∠DEF=1×
,EF=DEcos∠DEF=1× =
=
∴OF=OE+EF=1+ =
=
∴ ;(4分)
;(4分)
点评:本题利用了翻折的性质和锐角三角函数求解.
(2)过点D作DF⊥AO,则由三角函数的概念可求得EF、DF的值,从而得到点D的坐标.
解答:解:(1)由题意知,∠ACO=60°,OC=
 ,
,∴∠ECO=∠DCE=30°,OE=OCtan30°=1
∴点E(-1,0),点C(0,
 )
)设CE的解析式为y=kx+
 ,
,把点E的坐标代入得:0=-k+
 ,
,∴k=
 ,
,∴CE的解析式为:
 ;(4分)
;(4分)
(2)过点D作DF⊥AO,
由题意知DE=OE=1,∠DEF=∠DEC=∠CEO=60°,
∴DF=DEsin∠DEF=1×
 =
= ,EF=DEcos∠DEF=1×
,EF=DEcos∠DEF=1× =
=
∴OF=OE+EF=1+
 =
=
∴
 ;(4分)
;(4分)点评:本题利用了翻折的性质和锐角三角函数求解.

练习册系列答案
相关题目
 ,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
,∠CAO=30°.将Rt△OAC折叠,使OC边落在AC边上,点O与点D重合,折痕为CE.
 (x>0)的图象上,且横坐标为2.若将点P先向右平移两个单位,再向上平移一个单位后所得图象为点P′.则经过点P'的反比例函数图象的解析式是 .
(x>0)的图象上,且横坐标为2.若将点P先向右平移两个单位,再向上平移一个单位后所得图象为点P′.则经过点P'的反比例函数图象的解析式是 .