Question

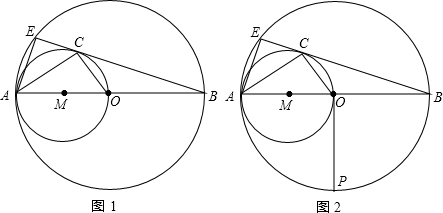
已知AB为⊙O直径，以OA为直径作⊙M．过B作⊙M得切线BC，切点为C，交⊙O于E．
（1）在图中过点B作⊙M作另一条切线BD，切点为点D（用尺规作图，保留作图痕迹，不写作法，不用证明）；
（2）证明：∠EAC=∠OCB；
（3）若AB=4，在图2中过O作OP⊥AB交⊙O于P，交⊙M的切线BD于N，求BN的值．

Answer 1

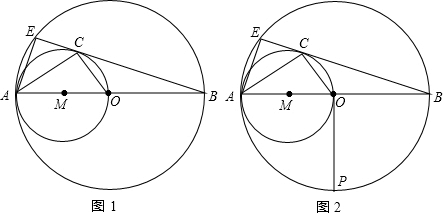
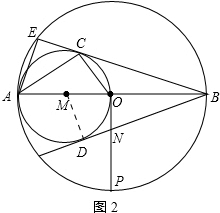（1）解：以MB为直径作圆，与⊙M相交于点D，直线BD即为另一条切线．

（2）证明：∵BC切圆与点C，
∴∠OCB=∠OAC，∠ECA=∠COA；
∵OA、AB分别为⊙M、⊙O的直径
∴∠AEC=∠ACO=90°，
∵∠EAC+∠ECA=90°，∠OAC+∠COA=90°，
∴∠EAC=∠OAC=∠OCB．

（3）解：连接DM，则∠BDM=90°在Rt△BDM中，BD=2．
∵△BON∽△BDM，
∴，
∴，
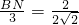∴BN=．
分析：（1）以MB为直径作圆，与⊙M相交于点D，直线BD即为另一条切线．
（2）根据BC切圆与点C，得到∠OCB=∠OAC、∠ECA=∠COA；再根据OA、AB分别为⊙M、⊙O的直径得到∠AEC=∠ACO=90°，从而得到∠EAC=∠OAC=OCB；
（3）连接DM，则可以得到∠BDM=90°，然后利用△BON∽△BDM列出比例式求得BN的长即可．
点评：本题考查了切线的性质、圆周角定理及相似三角形的判定及性质，比较复杂，是一道难题．