题目内容
(本题满分10分)已知AB为⊙O直径,以OA为直径作⊙M。过B作⊙M得切线BC,切点为C,交⊙O于E。
(1)在图中过点B作⊙M作另一条切线BD,切点为点D(用尺规作图,保留作图痕迹,不写作法,不用证明);
(2)证明:∠EAC=∠OCB;
(3)若AB=4,在图2中过O作OP⊥AB交⊙O于P,交⊙M的切线BD于N,求BN的值。

【答案】
(1)以MB为直径作圆,与⊙M相交于点D,直线BD即为另一条切线。
(2)证明:∵BC切圆与点C,所以有∠OCB=∠OAC,∠ECA=∠COA;
∵OA、AB分别为⊙M、⊙O的直径 ∴∠AEC=∠ACO=90°,
∵∠EAC+∠ECA=90°,∠OAC+∠COA=90°,∴∠EAC=∠OAC= OCB
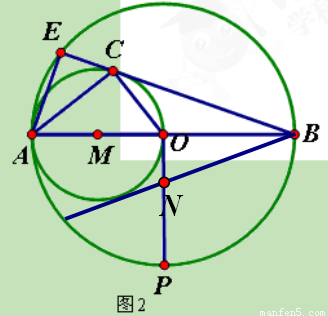
(3)连结DM,则∠BDM=90°在Rt△BDM中,BD=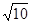 .
.
∵△BON∽△BDM
∴ ∴
∴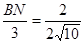 ∴BN=
∴BN=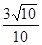 。
。
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 图象与x轴交点坐标;
图象与x轴交点坐标; 的两条高
的两条高 相交于点
相交于点 ,且
,且
 的角平分线上,并说明理由.
的角平分线上,并说明理由.
 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象.
 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离