题目内容
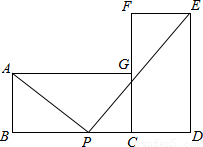
 如图,矩形ABCG与矩形CDEF全等,且AB=2,BC=4,点B、C、D在同一条直线上,点P在线段BD上移动,当BP=
如图,矩形ABCG与矩形CDEF全等,且AB=2,BC=4,点B、C、D在同一条直线上,点P在线段BD上移动,当BP=2或4
2或4
时,∠APE为直角.分析:利用当BP=x时,∠APE为直角,根据相似三角形的性质得出△ABP∽△PDE,进而求出x的值,即可得出答案.
解答:解:设当BP=x时,∠APE为直角,
∵AB=2,BC=4,
∴当∠APB+∠EPD=90°,∵∠BAP+∠APB=90°,
∴∠BAP=∠EPD,
∵∠ABP=∠EDP,
∴△ABP∽△PDE,
∴
=
,
即
=
,
解得:x=2或4,
故点P在线段BD上移动,当BP=2或4时,∠APE为直角.
故答案为:2或4.
∵AB=2,BC=4,
∴当∠APB+∠EPD=90°,∵∠BAP+∠APB=90°,
∴∠BAP=∠EPD,
∵∠ABP=∠EDP,
∴△ABP∽△PDE,
∴
| AB |
| PD |
| BP |
| DE |
即
| 2 |
| 6-x |
| x |
| 4 |
解得:x=2或4,
故点P在线段BD上移动,当BP=2或4时,∠APE为直角.
故答案为:2或4.
点评:此题主要考查了相似三角形的判定与性质以及一元二次方程的解法,根据已知得出△ABP∽△PDE是解题关键.

练习册系列答案
相关题目
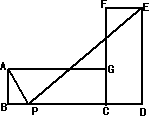
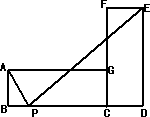
 如图,矩形ABCG与矩形CDEF全等,且AB=2,BC=4,点B、C、D在同一条直线上,点P在线段BD上移动,当BP=________时,∠APE为直角.
如图,矩形ABCG与矩形CDEF全等,且AB=2,BC=4,点B、C、D在同一条直线上,点P在线段BD上移动,当BP=________时,∠APE为直角.