题目内容
用19米长的铝合金条制成如图所示的矩形窗框ACDF．其中BE、GH均是铝合金制成的格条，且BE∥AF，GH⊥CD，EF=0.5m．设AF的长为x（单位：米），AC的长为y（单位：米）．
（1）求y与x的函数关系式（不必写出x 的取值范围）；
（2）若这个矩形窗框ACDF的面积等于10平方米，且AF＜AC，求出此时AF的长．
解：（1）在矩形ACDF中，∵∠A=90°，AB∥EF，AF∥BE，∴四边形ABEF是矩形，
∴EF=AB=0.5米．GH⊥CD，∴∠CHG=90°=∠C=∠CBG，
∴四边形BCHG是矩形，同理四边形DEGH是矩形．
∵BC=HG=DE=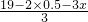
=6-x，AC=BC+AB，
∴y=6-x+0.5=-x+
．
（2）依题意得（-x+）x=10，解得
x1=
，x2=4，AF＜AC，
∴x＜-x+，即x＜
，
∴AF=米，
即当四边形的面积等于10平方米时，AF的长等于米．
分析：（1）可证明四边形BCHG、四边形DEGH、四边形ABEF是矩形．由图得出BC，从而得出用含x的代数式表示y即可；
（2）根据这个矩形窗框ACDF的面积等于AF•AC，再解方程即可．
点评：本题考查了矩形的判定和性质，以及一元二次方程的应用，是基础知识要熟练掌握．
∴EF=AB=0.5米．GH⊥CD，∴∠CHG=90°=∠C=∠CBG，
∴四边形BCHG是矩形，同理四边形DEGH是矩形．
∵BC=HG=DE=
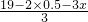=6-x，AC=BC+AB，∴y=6-x+0.5=-x+
．（2）依题意得（-x+
）x=10，解得x1=
，x2=4，AF＜AC，∴x＜-x+
，即x＜，∴AF=
米，即当四边形的面积等于10平方米时，AF的长等于
米．分析：（1）可证明四边形BCHG、四边形DEGH、四边形ABEF是矩形．由图得出BC，从而得出用含x的代数式表示y即可；
（2）根据这个矩形窗框ACDF的面积等于AF•AC，再解方程即可．
点评：本题考查了矩形的判定和性质，以及一元二次方程的应用，是基础知识要熟练掌握．
练习册系列答案
相关题目
（2011•南岗区一模）用19米长的铝合金条制成如图所示的矩形窗框ACDF．其中BE、GH均是铝合金制成的格条，且BE∥AF，GH⊥CD，EF=0.5m．设AF的长为x（单位：米），AC的长为y（单位：米）．
用19米长的铝合金条制成如图所示的矩形窗框，CD长表示窗框的宽，EF=0.5米．（铝合金条的宽度忽略不计）
用19米长的铝合金条制成如图所示的矩形窗框，CD长表示窗框的宽，EF=0.5米．（铝合金条的宽度忽略不计）