题目内容
 用19米长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5米.(铝合金条的宽度忽略不计)
用19米长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5米.(铝合金条的宽度忽略不计)(1)求窗框的透光面积S(平方米)之间的函数关系式;
(2)如何设计才能使窗框的透光面积最大?最大面积为多少?
(3)当窗框的面积不小于10平方米时,试结合函数的图象,直接写出x的取值范围.
分析:(1)可证明四边形BCHG、四边形DEGH、四边形ABEF是矩形.由图得出BC以及AC,从而得出用含x的代数式表示S即可;
(2)根据(1)关系式利用公式法求出最值即可,
(3)根据当s=10时解方程即可得出图象上点的坐标,进而求出与x轴交点坐标,得出图象即可得出x的取值范围.
(2)根据(1)关系式利用公式法求出最值即可,
(3)根据当s=10时解方程即可得出图象上点的坐标,进而求出与x轴交点坐标,得出图象即可得出x的取值范围.
解答:解:(1)在矩形ACDF中,∵∠A=90°,AB∥EF,AF∥BE,∴四边形ABEF是矩形,
∴EF=AB=0.5米.GH⊥CD,∴∠CHG=90°=∠C=∠CBG,
∴四边形BCHG是矩形,同理四边形DEGH是矩形.
设AF=x,
∵BC=HG=DE=
=6-x,AC=BC+AB,
∴y=6-x+0.5=-x+
.
S=xy=(-x+
)x=-x 2+
x,
(2)依题意得S=-x 2+
x,
当x=-
=-
=
时,
S最大=
=
=
;
(3)当(-x+
)x=10,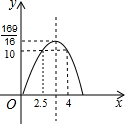
解得x1=
,x2=4,
当s=0,则0=-x 2+
x,
解得:x1=0,x2=6.5,
图象与x轴交点坐标为:(0,0),(6.5,0),再利用图象顶点坐标为:(
,
),
如图所示:
当窗框的面积不小于10平方米时,结合函数的图象得出x的取值范围是:2.5≤x≤4.
∴EF=AB=0.5米.GH⊥CD,∴∠CHG=90°=∠C=∠CBG,
∴四边形BCHG是矩形,同理四边形DEGH是矩形.
设AF=x,
∵BC=HG=DE=
| 19-2×0.5-3x |
| 3 |
∴y=6-x+0.5=-x+
| 13 |
| 2 |
S=xy=(-x+
| 13 |
| 2 |
| 13 |
| 2 |
(2)依题意得S=-x 2+
| 13 |
| 2 |
当x=-
| b |
| 2a |
| ||
| 2×(-1) |
| 13 |
| 4 |
S最大=
| 4ac-b2 |
| 4a |
0-
| ||
| 4×(-1) |
| 169 |
| 16 |
(3)当(-x+
| 13 |
| 2 |

解得x1=
| 5 |
| 2 |
当s=0,则0=-x 2+
| 13 |
| 2 |
解得:x1=0,x2=6.5,
图象与x轴交点坐标为:(0,0),(6.5,0),再利用图象顶点坐标为:(
| 13 |
| 4 |
| 169 |
| 16 |
如图所示:
当窗框的面积不小于10平方米时,结合函数的图象得出x的取值范围是:2.5≤x≤4.
点评:本题考查了二次函数的应用以及二次函数最值求法以及一元二次方程的应用等知识,根据图象得出x的取值范围是解题关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 (2011•南岗区一模)用19米长的铝合金条制成如图所示的矩形窗框ACDF.其中BE、GH均是铝合金制成的格条,且BE∥AF,GH⊥CD,EF=0.5m.设AF的长为x(单位:米),AC的长为y(单位:米).
(2011•南岗区一模)用19米长的铝合金条制成如图所示的矩形窗框ACDF.其中BE、GH均是铝合金制成的格条,且BE∥AF,GH⊥CD,EF=0.5m.设AF的长为x(单位:米),AC的长为y(单位:米). 用19米长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5米.(铝合金条的宽度忽略不计)
用19米长的铝合金条制成如图所示的矩形窗框,CD长表示窗框的宽,EF=0.5米.(铝合金条的宽度忽略不计) 用19米长的铝合金条制成如图所示的矩形窗框ACDF.其中BE、GH均是铝合金制成的格条,且BE∥AF,GH⊥CD,EF=0.5m.设AF的长为x(单位:米),AC的长为y(单位:米).
用19米长的铝合金条制成如图所示的矩形窗框ACDF.其中BE、GH均是铝合金制成的格条,且BE∥AF,GH⊥CD,EF=0.5m.设AF的长为x(单位:米),AC的长为y(单位:米).